2

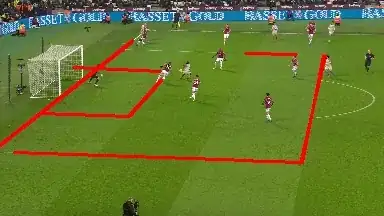
I am trying to obtain an Homography of a soccer image shot by a broadcasting camera. The original picture:

1

I then proceed to find field lines, resulting in the following:

2

From what I understand, at least 4 points need to be detected. From the detected line, I should easily obtain 4 points by intersection of the lines. (I will extend the detected lines so they actually intersect)

The detected points can then be projected to another image. Since I do not have another image, I believe I should use a field model, like the one below.

3

Since field dimensions are known, every intersection point of the field model in world coordinates are known. For example: the middle of the field can be set to (0,0) (in meters). The top right of the field will then be (52.5,34) (in meters).

Now how do I set those world coordinates on the image?

Rodrigo de Azevedo
  • 1
Stan
  • 133
  • Any particiular place are you looking at ? Are you collect all of the soccer stadiums ? –  Feb 22 '19 at 15:15
  • Ultimately, I am developing a program that can extract camera parameters from broadcasting cameras. To compute intrinsic and extrinsic parameters, I need to obtain an homography. So this is just a sample image, as I will run this in multiple stadiums/matches. For each particular stadium, measurements can easily be found. So I know real world coordanites of the detected points, but a program obviously can not because it does not know at what part of the field it is looking at. –  Feb 22 '19 at 15:18
  • Ok. I am not familiar with the Homography. But you said you got the real world coordinates such as latitude and longitude, correct . –  Feb 22 '19 at 15:29

1 Answers1

2

Not exactly homography, but you could just use georeferencing in QGIS or ArcGIS, and look through the different projections. I've tried something similar with hockey, and georeferencing when players shot goals from.

from my previous reddit post on the subject:
I created a 200ft x 80ft rectangle over PNC arena in ArcGIS Pro using the North Carolina State Plane NAD 83 2011 revision, plus two 80ft x 11ft boxes at each end to make georeferencing the diagram in the official 2018-19 NHL Rulebook. Then, I took the screen grab of the play, and georeferenced the extremely oblique image to the georeferenced rink using a spline georeferencing. Larkin's goal was roughly 181 ft, 19ft short of the entire length of the ice.

enter image description here

  • Thanks for your answer. However, I can not use this. I NEED to obtain an homography, so this unfortunately does not answer my question. – Stan Feb 23 '19 at 09:11