Does "P does not imply Q" mean that (P → Q) is not always true?

Question

"P implies Q" means that if P is true then Q must be true. We also know that "P implies Q" is false when P is true and Q is false.

Now, one answer that I have seen on this site says that "P does not imply Q" means "$\lnot$(P $\to$ Q)". But "P does not imply Q" normally means that if P is true then Q may or may not be true; in other words, "P does not imply Q" normally means that (P $\to$ Q) is not always true.

Where is my misunderstanding? Please tell me what "P does not imply Q" actually means, hopefully with a truth table clarification. If ambiguity exists somewhere here, then please let me know the circumstances in which care should be taken.

Answer 1

The issue you seem to be having is confusing truth with validity. In particular, you are confusing $\neg(P\to Q)$ being true (and thus $P\to Q$ being false) with $P\to Q$ being invalid. (Instead of "valid", it is more likely that you've seen "is a tautology".)

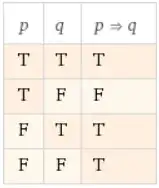
When we're going through a logical argument, the atomic propositions, $P$ and $Q$ in this case, are known or assumed to hold some particular truth values. This is typically formalized by saying we have some truth assignment for all the atomic propositions. We can then calculate what the truth value for a whole formula, e.g. $P\to Q$, is given that truth assignment.

In early logic classes, you are often being asked to show that a given formula is or is not a tautology, i.e. that it is or is not valid. Doing this means showing that the formula is true for all truth assignments. As I said in the first paragraph, you seem to be confusing "$\varphi$ is false" with "$\varphi$ is invalid", probably because you've been given exercises to show that some formula is "false" that should have been stated as, "show that some formula is not a tautology".

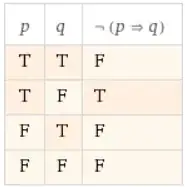
So $\neg(P\to Q)$ being valid doesn't mean $P\to Q$ is invalid (which is what "not always true" means); it would mean that $P\to Q$ is always false. Since $P\to Q$ is not always false, neither $P\to Q$ nor $\neg(P\to Q)$ are valid. This situation is sometimes described as $P\to Q$ being contingent. On the other hand, if $\neg(P\to Q)$ is true with respect to some truth assigment, then $P\to Q$ is false with respect to the same truth assignment by definition of $\neg$. Two (propositional) formulas are (semantically) equivalent if they have the same truth value for each truth assignment. Again, by definition of $\neg$, this will never happen with a formula and its negation.

Answer 2

The Meaning of IMPLIES in Classical Logic

If $p$ and $q$ are logical propositions of unambiguous truth values (either true or false), then

• $p \implies q$ does not mean that $p$ causes $q$, or that $q$ causes $p$.

• $p \implies q$ means only that, at the moment, it is false that both $p$ is true and $q$ is false. No other logical connection is assumed.

Example: Let $p$ be the proposition that it is cloudy. Let $q$ be the proposition that it is raining. If, at the moment, $p$ is false (it is not raining) and $q$ is false (it is not cloudy), then we can infer that $p\implies q$, i.e. that if it is raining, then it is cloudy.

Yes, it is counter-intuitive, but this form of logical implication works as the basis for most if not all of modern mathematics. There is no passage of time or cause and effect in mathematics. These are in the realms of science.

Compare the Truth Tables

Source

Note that $p\implies q$ is false if and only if $p$ is true and $q$ is false (see line 2).

Also, $\neg (p \implies q)$ is true if and only if $p$ is true and $q$ is false (see line 2).

Other interesting points about the truth table for $p \implies q\space$:

• If $p$ is false then $p\implies q$ regardless of the truth value of $q$ (see lines 3 and 4).
• If $q$ is true then $p\implies q$ regardless of the truth value of $p$ (see lines 1 and 3).

Answer 3

But "P does not imply Q" normally means that if P is true then Q may or may not be true; in other words, "P does not imply Q" normally means that (P $\to$ Q) is not always true.

Good question! I wrote a fuller explanation at Not necessarily imply, but the short of it is that you are conflating propositional and first-order logic, and not noticing the implicit universal quantification in the first two of these equivalent sentences:

• $P(x){\kern.6em\not\kern-.6em\implies} Q(x)$
• it is false that $\big(P(x){\implies} Q(x)\big)$
• $P(x)$ does not universally imply $Q(x)$
• $\lnot\forall x\; \big(P(x)\to Q(x)\big)$
• $\exists x \;\lnot\big(P(x)\to Q(x)\big)$
• for some $x,\,$ $P(x)$ is true and $Q(x)$ is false.

These sentences do each imply that $\big(P(x)\to Q(x)\big)$ is not true for every value of $x.$

Please tell me what "P does not imply Q" actually means, hopefully with a truth table clarification.

A truth table can only clarify that these sentences are equivalent:

• $P{\kern.6em\not\kern-.6em\implies} Q$
• it is false that $\big(P{\implies} Q\big)$
• $P$ does not imply $Q$
• $\lnot \big(P\to Q\big)$
• $P$ is true and $Q$ is false.

So, all this is correct:

"P implies Q" means that if P is true then Q must be true. We also know that "P implies Q" is false when P is true and Q is false.

Now, one answer that I have seen on this site says that "P does not imply Q" means "$\lnot$(P $\to$ Q)".