1

I was wondering:

What are the real zeros of the function $$x^{n+1}-2x^n+1$$ where $n$ is a positive integer?

Obviously, there is a zero at $x=1$. But, if $n$ is even, there are two other real zeros, one negative and one positive; if $n$ is odd, there is one other real zero, and it is positive.

I know there may not be a closed form to find this, but if there is, the derivation and answer would be appreciated. If the negative root cannot be found, the positive root would be enough.

Blue
  • 75,673
Varun Vejalla
  • 8,873
  • I wouldn't at all be surprised if for most $n$, the roots cannot be expressed in terms of radicals. On the other hand, it's very likely that asymptotic series exist for the roots, e.g. $x = 2 - 2^{-n} + O(2^{-2n})$ (rough heuristic calculation, not checked) - though such series are usually not considered closed form expressions. – Daniel Schepler Feb 15 '19 at 01:01
  • About irreducibility, a very close issue : https://math.stackexchange.com/q/393646 – Jean Marie Feb 15 '19 at 07:52

1 Answers1

4

Set $x=\frac{1}{X}$ (which is possible because $x=0$ isn't a solution) giving

$$X^{n+1}-2X+1=0.$$

It means that, in this way, we are looking for the abscissas of intersection points of power curve with equation $Y=X^{n+1}$ with straight line having equation $Y=2X-1$.

Moreover, there is always an intersection point at $(X,Y)=(1,1)$.

This provides a clear qualitative view of what happens, with an easy discussion between the cases $n$ even/ $n$ odd.

Let us illustrate the case where $n$ is odd :

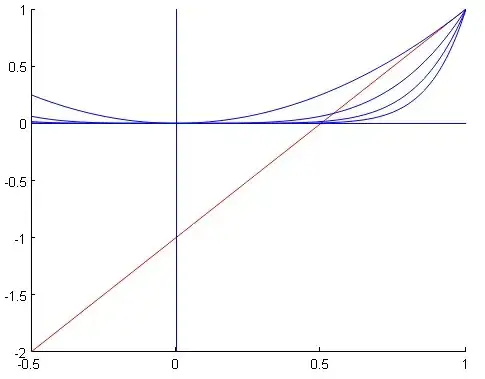
enter image description here

Fig. 1 : Polynomial curves with equations $Y=X^{(n+1)}, \ \ n=1,3,5,7$ intersect straight line $Y=2X-1$ in two points points with abscissas 1 and $\tfrac12+\varepsilon_n$.

We see in particular that the second root has the form

$$X=\tfrac12+\varepsilon_n \tag{1}$$

It is solution of the following equation :

$$Y=(\tfrac12+\varepsilon_n)^{\tfrac{1}{n+1}}=2(\tfrac{1}{2}+\varepsilon_n)-1$$

$$\tfrac{1}{a}(1+\tfrac12\varepsilon_n)^{\tfrac{1}{n+1}}=2\varepsilon_n \ \ \text{with} \ \ a:=2^{n+1}$$

$$(1+\tfrac12\varepsilon_n)^{\tfrac{1}{n+1}}=2a\varepsilon_n$$

Taking a first order approximation of the LHS :

$$1+\tfrac{1}{2(n+1)}\varepsilon_n\approx 2a\varepsilon_n $$

Thus $\varepsilon_n \approx \frac{1}{2a-\tfrac{1}{2(n+1)}}\tag{2}$

plugging (2) into (1) (and taking $x=\tfrac{1}{X}$) gives an approximation of the root which is that of @Daniel Schepler.

Remark : A second transformation could be interesting by taking the reciprocal functions, i.e., considering the intersection points between curves with equations

$$Y=X^{1/(n+1)} \ \ \ \text{and} \ \ \ Y=\frac12(X+1)$$

with graphical representation symmetrical of the one given above by exchanging the rôles of $X$ and $Y$ axes (it could be useful in particular for iteration schemes such as Newton's method).

Jean Marie
  • 81,803