What is the smallest number of $45^\circ$–$60^\circ$–$75^\circ$ triangles in non-trivial substitution tiling?

Question

Let base = $45^\circ$–$60^\circ$–$75^\circ$ triangle.

Over at What is the smallest number of bases that a square can be divided into? it was determined that 23 base were needed to make a $45^\circ$–$45^\circ$–$90^\circ$ triangle.

How about non-trivial dissections of base into similar triangles? Start with base and divide it into smaller copies of base. Ideally the method should be specific to base and wouldn't work with other triangles. Also, at least one of the internal triangles should have no edges parallel to the original triangle.

What are the simplest non-trivial dissections of base into similar triangles?

Answer 1

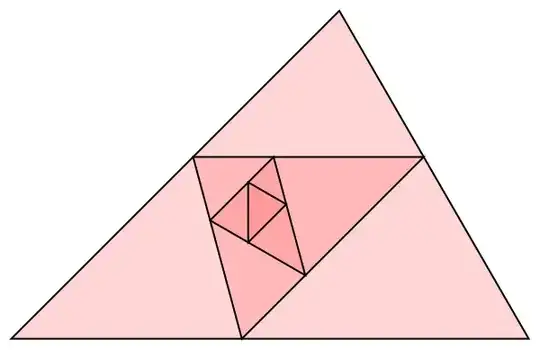
Hmm... This doesn't exactly fit your criterion in that it's not unique to the $45^∘–60^∘–75^∘$ triangle, but the central triangle here has no edges parallel to the edges of the original triangle.

The vertices are: $$ \begin{array}{ccc} \{0,0\} \\ \{1,0\} \\ \left\{\frac{1}{2} \left(3-\sqrt{3}\right),\frac{1}{2} \left(3-\sqrt{3}\right)\right\} \\ \left\{\frac{1}{22} \left(21-2 \sqrt{3}\right),\frac{1}{22} \left(6+\sqrt{3}\right)\right\} \\ \left\{-\frac{3}{22} \left(-5+\sqrt{3}\right),0\right\} \\ \left\{\frac{1}{22} \left(6+\sqrt{3}\right),\frac{1}{22} \left(6+\sqrt{3}\right)\right\} \\ \left\{\frac{1}{286} \left(237-43 \sqrt{3}\right),\frac{1}{143} \left(21-2 \sqrt{3}\right)\right\} \\ \left\{\frac{1}{286} \left(216-41 \sqrt{3}\right),\frac{1}{22} \left(6+\sqrt{3}\right)\right\} \\ \left\{\frac{1}{286} \left(174-37 \sqrt{3}\right),\frac{1}{286} \left(36+17 \sqrt{3}\right)\right\} \\ \left\{\frac{996-197 \sqrt{3}}{1430},\frac{192+43 \sqrt{3}}{1430}\right\} \\ \left\{\frac{996-197 \sqrt{3}}{1430},\frac{306+73 \sqrt{3}}{1430}\right\} \\ \left\{\frac{1}{130} \left(102-19 \sqrt{3}\right),\frac{318+31 \sqrt{3}}{1430}\right\} \\ \end{array} $$

This is based on the three other four-self-similar-triangle dissections beyond the usual midpoints-of-the-sides one: