1

I have an image of a rectangle that is noisy (perspective image).

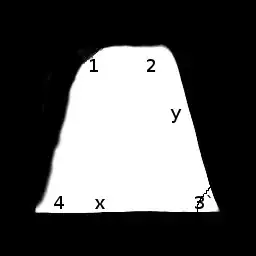
paper image

I know the value of $x$, $y$, and angle $3$. Angles "$2$" and "$4$" are not accurate. Also, I know the real rectangle size. The angle "$1$" is noisy. I want to complete the rectangle and calculate the angle "$4$" in the image.

Having this information, can I calculate the angle "$4$" and complete the rectangle?

simonet
  • 467
Mostafa Farzane
  • 11
  • 1

2 Answers2

0

Can I calculate the angel "4" and complete the rectangle?

Short answer: no.

As discussed here, a perspective transformation is uniquely defined by four points and their images. So you can take any rectangle as preimage, guess positions 2, 3, 4 from your image, place point 1 anywhere and still find a projective transformation to achieve this mapping. Knowing 2, 3, 4 and the original rectangle does not add value towards knowing where 1 has to be. Assuming perspective rectangle means a rectangle under an arbitrary projective transformation, which is how I'd read the question.

MvG
  • 42,596
0

My suggestion is to estimate the value of angle $4$ in the following steps:

  1. Detect the contour that delimits the rectangle in the image. Since your image has a high contrast, it should be enough to use a marching squares algorithm with a global threshold.

  2. Process the contour to split it into 4 contours, one for each edge. You could split, e.g., the contour with the four extreme points (most up-left, most up-right, most down-left, most down-right).

  3. For every such contour, estimate the best fitting line, i.e., the line that interpolates the points of the edge contour in a "best" way. For this step you could use a RANSAC algorithm.

  4. Finally, estimate the angle $4$ by computing the angle between the two lines that interpolate the edges incident in angle $4$.

simonet
  • 467