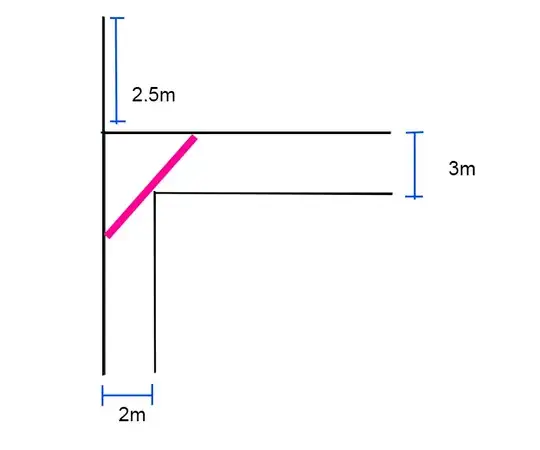
I want to calculate the maximum measurements that a wooden board can have, to pass through the corner
The first thing I did was to make a problem easier, when the table does not have width, with similar triangles, calculating the red line (the maximum length that the table can have). I got a function and I minimized it.
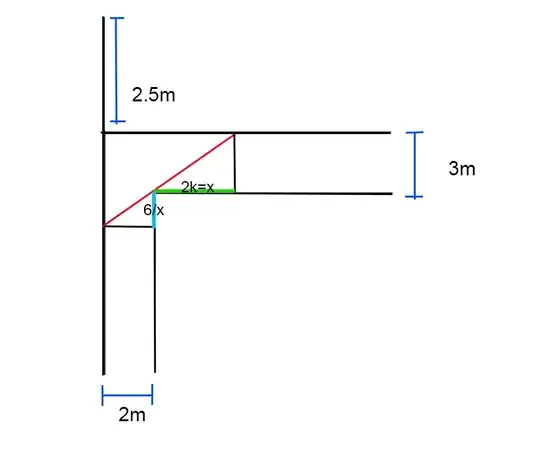
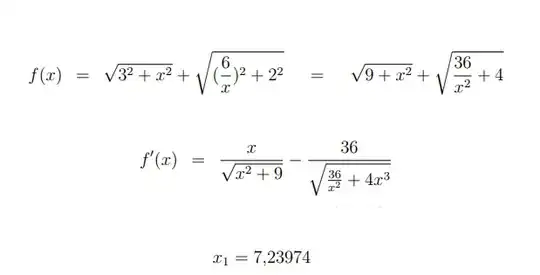
But I do not know how to do when the wood has an area. I imagine it is a minimization problem with two variables, but I do not know what function to use, help me please