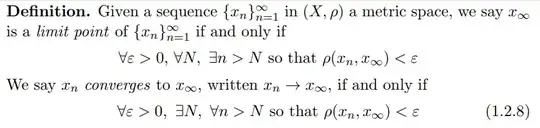2

Some background (all of this is from Barry Simon's "Real Analysis - A comprehensive course in analysis - vol 1"):

Reading both definitions I can see the difference between weakly sequentially compact and sequentially compact, but I can't find an example of a topological space which is weakly sequentially compact but not sequentially compact or at least one space where we have a sequence with at least one limit point but which doesn't have any convergent subsequence.

Here are some potential counter examples some friends and I thought of but didn't work:

Consider $\mathbb{N} \times \{0, 1\}$ where $\mathbb{N}$ has the discrete topology and the latter the indiscrete one. Now, the sequence:

$(1, 0), (1, 1), (2, 0), (2, 1), \cdots$

clearly has no limit point. It's also pretty clear that it doesn't have any convergent subsequence.

Community
  • 1
Matheus Andrade
  • 6,773

2 Answers2

3

$\{0,1\}^{\mathbb{R}}$ is weakly sequentially compact (it's even compact Hausdorff which implies that property), but it has sequences without convergent subsequences.

$\beta \omega$, the Cech-Stone compactification of the countable discrete space $\omega$ is another example, for the same reasons. The sequence $x_n = n \in \omega$ is a sequence without a convergent subsequence.

"Weakly sequentially compact" is a confusing name IMHO, just call it countably compact (every countable open cover has a finite subcover), to which it is equivalent. I show this fact in my answer here.

Henno Brandsma
  • 242,131
  • Thanks for the answer and the suggestion at the end! Could you edit it to include at least one example of a sequence in ${0, 1}^{\mathbb{R}}$ which has no convergent subsequence (I haven't worked that much with function spaces yet)? – Matheus Andrade Feb 08 '19 at 22:53
  • I've managed to come up with an example of a sequence in ${0, 1}^{\mathbb{R}}$ with no convergent sub-sequence, but I've yet to show that any sequence has a limit point. I know compactness and Hausdorff together mean that it's true, but I can't use compactness yet so I would like to do it the usual way (proving it satisfies the definition) but it's been hard. Could you help? – Matheus Andrade Feb 09 '19 at 06:37
  • @MatheusAndrade you need the compactness of ${0,1}^\mathbb{R}$, so Tychonoff's theorem, you cannot show it directly from the definitions I think. You can deduce it from the compactness of the countable subproducts, if that helps. – Henno Brandsma Feb 09 '19 at 06:44
  • It does indeed. Thanks for taking the time! – Matheus Andrade Feb 09 '19 at 07:29
  • 1
    @MatheusAndrade I exhibit such a sequence here in the homeomorphic space ${0,1}^{(2^\mathbb{N})}$ – Henno Brandsma Feb 09 '19 at 09:16
0

I would try the interval $[-1,1]$ with two origins. The sequence $\{1/n\}$ has two limit points (the two origins), but no convergent subsequence.

TiddSchmod
  • 416