Christiaan Huygens accurately calculated the distance from Earth to the Sun in 1659 to be 1.023 times our modern figure of 1AU=1.495978707e11 metres. They say he noticed, like Galileo before him, that Venus underwent phases just like the moon does. So, he reasoned, when Venus is half-lit, like a quarter moon, then the Sun, Venus and the Earth form a right triangle. Thus, if we knew the distance from the Earth to Venus at this moment of configuration, then we can calculate the distance from the Sun to the Earth using trigonometry. But, I need to prove that the maximum deflection of the angle between Venus and the Sun indicates Venus is half-lit, because I have to use a telescope on Earth to measure the angle and it's difficult to see enough detail. Please see the attached diagram and tell me I'm on the right track. Although the diagram is not exactly to scale, both Venus and the Earth are moving in a counter clockwise direction and Venus has a higher angular velocity than the Earth. 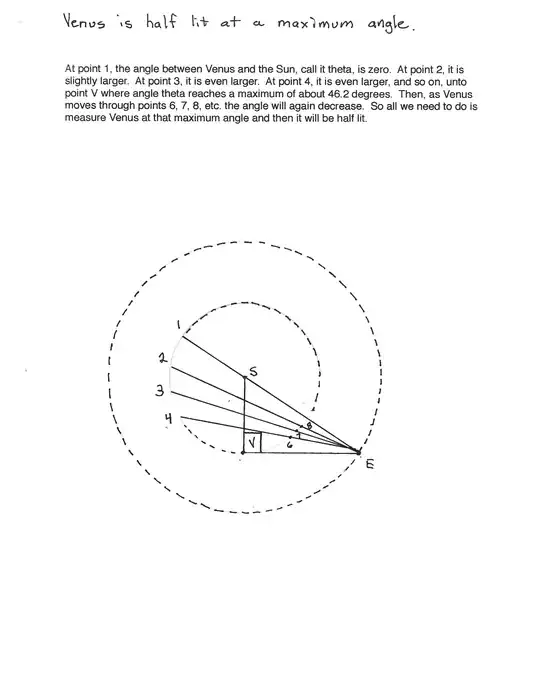
- 872
1 Answers
Draw a small circle at the dot labelled $V$. The line from the earth to that circle bisects it, so Venus is half-lit.
Post-comment addition The question said "I need to prove that [when venus is at maximum deflection from the sun], Venus is half-lit." But apparently you needed more than this -- you need to "prove that the angle between the sun and venus is at a maximum magnitude."
I don't think you need to prove this.
I showed that if the angle is at a maximum, then venus is half-lit. That's what you really need.
I suppose you might also need this: if the angle is at a maximum, then the triangle from earth to venus to sun has a right angle at $V$. So let's prove that (assuming the orbit of venus and the earth are both circular).
Here's a proof: Look at your picture. The line from $E$ through $V$ has the property that exactly one point of venus's orbit (labelled "V") is on that line, and all other orbit points are to the right (sun side) of it (as seen from the earth), so the sun-earth-venus angle is smaller for all those points. Hence this particular line is the one where the sun-earth-venus angle is greatest. Furthermore, it's a line containing exactly one point of a circle (venus's orbit), hence is a tangent line to that circle. And any tangent line to a circle is perpendicular to the circle-radius (the line SV in your diagram) at the point of tangency (V in your diagram). So we're done.
- 93,729
-
Yes, but I need to prove the angle between the Sun and Venus is at a maximum magnitude. Does that prove that? – Michael Lee Feb 07 '19 at 04:21
-
See post-comment addition. – John Hughes Feb 07 '19 at 11:25
-
Excellent! I began to reason that in order for the angle to be bigger, Venus would need to be in a larger orbit than what it already is. – Michael Lee Feb 07 '19 at 15:38
-
I think that there's probably an argument to be made like that as well, but I'm not sure that the 90-degree angle falls out of it easily. – John Hughes Feb 07 '19 at 16:07
-
I liked it enough to answer, but to be honest, the question didn't interest me a lot (which is my standard for "liking"); my guess is that a lot of other folks could have answered it too, and it also didn't interest them much. Sometimes we see questions like this -- things that are pretty basic to many of us, but someone like you needs an answer, and we provide it. (A good example: someone needs to know how approximate many bricks will be needed to pave an irregularly shaped area that's drawn for us.) Others "liking" is different from a question having merit (especially to the asker!). – John Hughes Feb 11 '19 at 22:49
-
Interesting John Hughes, what I find totally fascinating, most others find absolutely abhorrent. – Michael Lee Feb 12 '19 at 23:05
-
The person paving the garden area cares a lot about gardens, but you can't expect us to love gardens, too. I'm actually a bit interested in astronomy, but mostly for navigation, so this question almost hit the mark for me, but not quite. – John Hughes Feb 13 '19 at 02:43