I recently learned about the trigonometric functions of angles greater than $90$ degrees, and I'm having a hard time understanding the concept.
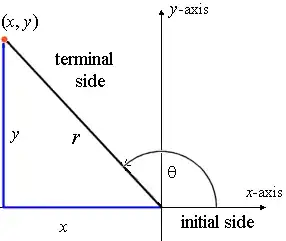
We worked with a diagram like this:
My teacher proceeded to tell the class that the sine of angle $\theta$ was equal to the ratio between the opposite side ($y$) and the hypotenuse ($r$).
I don't quite understand this logic. I'm familiar with trigonometric functions, but as I remember them, they applied to angles inside a right-triangle, not an angle outside of it. This seems counter-intuitive to me.
Shouldn't the sine ratio (or cosine, for that matter) represent the angle $180 - \theta$ located inside the right triangle, rather than outside of it? An explanation would be greatly appreciated, as this is a key part of our current unit.