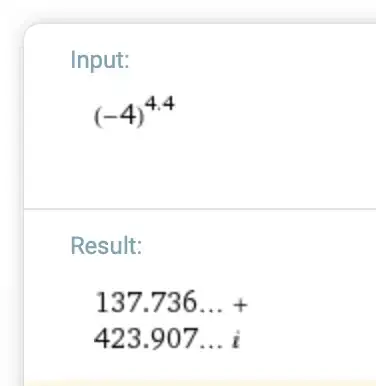
One would think that, since $4.4$ as a mixed fraction is ($22/5$), raising a number regardless of it being negative or positive would yield a real number. However, when plugging this equation into WolframAlpha, I keep getting an imaginary number.
Can someone help me understand? I plug the equation in like so: (-4)^4.4 and still get a nonreal answer. What is going on here?
Using Euler's formula you can represent every real number as having real and complex part
$$-4 = 4\cdot(\cos(\pi) + i\sin(\pi)) = 4\cdot e^{i\pi}$$
Now you can write exponentiation as follows
$$(-4)^{4.4} = (4\cdot e^{i\pi})^{4.4} = 4^{4.4}\cdot e^{4.4i\pi}$$
$$4^{4.4}\cdot e^{4.4i\pi} = 445.722\cdot e^{4.4i\pi} = 137.736 + 423.907i$$
and that is the number that Wolfram Alpha computed.
Alpha is not seeing $4.4$ as an exact rational, it is seeing it as a generic floating point number. As such it is evaluating $$(-4)^{4.4}=\exp(4.4 \ln(-4))$$ The $\ln(-4)$ has an imaginary part of $\pi i$ (plus some multiple of $2\pi i$) and that gets you into the complex realm. There are five complex fifth roots of $(-4)^{22}$ and Alpha is giving you one of them. Later it gives you all of them.
Yes, you can take odd integral roots of negative numbers, but Alpha doesn't realize that is what you want.
