Finding an Inverse of Restricted Gamma Function

Question

I don't know/haven't used LaTeX yet but I'll do my best to keep it simple,

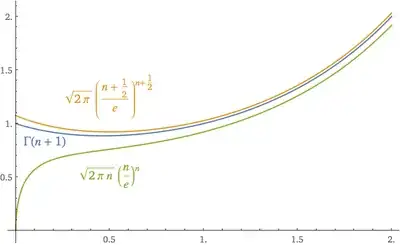
I'm working on my undergrad senior project and I'm trying to find an inverse function for f(x)=(x-1)! just in the positive reals. I was inspired to ask this question when in one of my probability classes my professor talked about how something like π! existed. Now, obviously, this isn't a 1:1 function so an inverse doesn't exist, but I first restricted the function just to x > 0 and then restricted it further after finding the minimum which is x=1.461632... or the positive root of the digamma function. You can see what I mean on this graph (the green one is what I'm trying to find the inverse of). After restricting the domain to x>1.461632... , the function is 1:1 and an inverse does exist.

This is where I'm stuck at.

I guess what I'm asking is that is there a way to find this inverse? I know that, for example, f^-1(120)=5 and f^-1(3(√π )/4)=2.5 but what of something like f^-1(25) or f^-1(e)? I've seen things like Stirling's Approximation and finding an inverse based off of that but I wanted to see if anybody else has any ideas of what I can do next.

Thank you for your time and let me know if you have any questions about my post.

Answer 1

Approximate Inverse

In this answer, the approximate inverse for $n!$ $$ n\sim e\exp\left(\operatorname{W}\left(\frac1{e}\log\left(\frac{n!}{\sqrt{2\pi}}\right)\right)\right)-\frac12\tag{1} $$ is given. This approximate inverse is gotten by inverting the approximation $$ n!\sim\sqrt{2\pi}\,\left(\frac{n+\frac12}e\right)^{n+\frac12}\tag2 $$ Comparing the asymptotic expansions $$ \begin{align} n! &=\sqrt{2\pi n}\,\left(\frac{n}e\right)^{n}\left(1+\frac1{12n}+\frac1{288n^2}+O\!\left(\frac1{n^3}\right)\right)\tag3\\ &=\sqrt{2\pi}\,\left(\frac{n+\frac12}e\right)^{n+\frac12}\left(1-\frac1{24n}+\frac{25}{1152n^2}+O\!\left(\frac1{n^3}\right)\right)\tag4 \end{align} $$ we see that, for large $n$, $(2)$ is an over-approximation, which has less than half the error of Stirling's formula. $$ \frac{\sqrt{2\pi}\,\left(\frac{n+\frac12}{\lower{2pt}e}\right)^{n+\frac12}-n!}{n!-\sqrt{2\pi n}\,\left(\frac{n}e\right)^{n}}=\frac12-\frac9{32n}+O\!\left(\frac1{n^2}\right)\tag5 $$ $(2)$ is also quite a bit better than Stirling for small $n$:

As $n\to-\frac12$, $(2)\to\sqrt{2\pi}$ instead of $\sqrt\pi$, but Stirling doesn't work at all for $n\lt0$.

---

Refining the Approximation

We can iterate the asymptotic series $$ \sqrt{2\pi}\,\left(\frac{n+\frac12}e\right)^{n+\frac12} =n!\scriptsize\left(1+\frac1{24n}-\frac{23}{1152n^2}+\frac{2957}{414720n^3}-\frac{8207}{7962624n^4}+O\!\left(\frac1{n^5}\right)\right)\tag6 $$ along with the exact inverse of the left hand side, given in $(1)$, to refine the approximation.

As in $(1)$, define $$ f(x)=e\exp\left(\operatorname{W}\left(\frac1{e}\log\left(\frac{x}{\sqrt{2\pi}}\right)\right)\right)-\frac12\tag7 $$ Start with $a_1=f(n!)$, then iterate $$ a_{k+1}=f\!\left(n!\scriptsize\left(1+\frac1{24a_k}-\frac{23}{1152a_k^2}+\frac{2957}{414720a_k^3}-\frac{8207}{7962624a_k^4}\right)\right)\tag8 $$ and then $$ \lim_{k\to\infty}a_k\sim n\tag9 $$ where the approximation in $(9)$ is much closer than simply applying $(1)$.

Answer 2

There is the algorithm by David W. Cantrell as described here. The idea is that we can use

$$g(x) = \sqrt{2\pi}{\left(\frac{x-1/2}{e}\right)^{x-1/2}} - c$$

as an approximation of $\Gamma(x)$. Here $c = \sqrt{2\pi}/e - \Gamma(k)$ where $k$ is the positive zero of the derivative of $\Gamma$. We can invert this function in terms of the Lambert $W$-function. First we set

$$L(x) = \ln\left(\frac{x+c}{\sqrt{2\pi}}\right)$$

and then we get

$$AIG(y) := g^{-1}(y) = \frac{L(x)}{W\left(\frac{L(x)}{e}\right)} + 1/2.$$

As the arguments increase the error gets very small, consider following evaluations:

$$\begin{array}{r|ll} N & AIG((N-1)!) & \text{error} \\ \hline 2 & \hphantom{1}2.02 & \hphantom{-}0.01 \\ 5 & \hphantom{1}4.995 & -0.001 \\ 10 & \hphantom{1}9.998 & -0.0002 \\ 20 & 19.9993 & -0.00004 \\ \end{array}$$

Answer 3

Bear in mind in reading this that I am an engineer, and this is just a non-rigorous sketch of what you could try.

Assuming you are allowed to use the Gamma Function integral defined for the positive reals only, then you can use this function to calculate the "Inverse Gamma Function" for the positive reals up to any desired cut off as long as you are willing utilize and prove the identity:

$$\sin(\pi z)=\frac{\pi z}{\Gamma(1-z)\Gamma(1+z)}\tag{1}$$

where $\Gamma(z)=\int_0^{\infty } e^{-t} t^{z-1} \, dt$ for $z>0$

Rearranging (1) we have

$$\frac{z}{\Gamma(1+z)}=\frac{ \Gamma(1-z) \sin(\pi z)}{\pi}=\left(\frac{1}{\Gamma(z)}\right)$$

You will immediately say that this only works for $0<z<1$ so it is not much use for your purpose, but we can write

$$\frac{z\prod _{k=1}^{n-1} (z+k)}{\Gamma(n+z)}=\frac{ \Gamma(n-z) \sin(\pi (z+n-1))}{\pi \prod _{k=1}^{n-1} (z-k)} =\left(\frac{1}{\Gamma(z)}\right)$$

where n is a positve integer $\ge 1$. Therefore you can now calculate your inverse Gamma Function with $z$ in the range $0<z<n$, without worrying about how to calculate negative factorials!

Edit 1: Lets push this a bit further and define a Pochammer Function approximation to the Gamma Function $\Gamma_P$

$$\Gamma_P(z)=\prod _{k=1}^{\lfloor z-1\rfloor } ((-\lfloor z-1\rfloor +z-1)+k)$$

where $\lfloor z\rfloor$ is the floor function on $z$ and

$$\Gamma(z)=\Gamma ((z-\lfloor z\rfloor )+1) \Gamma_P(z)$$

which gives $$\frac{\Gamma ((z-\lfloor z\rfloor )+1) \Gamma_P(n-z) \sin (\pi (n+z-1))}{\pi \prod _{k=1}^{n-1} (z-k)}\approx\left(\frac{1}{\Gamma(z)}\right)\tag{2}$$

with the true Gamma Function $\Gamma ((z-\lfloor z\rfloor )+1)$ now just used in the range $1\le ((z-\lfloor z\rfloor )+1) \le 2$

(Note: Equation 2 is approximate, and $n$ can be set to $1$, simplifying the formula - not sure about the origin of the error here need to review this when I have time)

I've plotted $\Gamma ((z-\lfloor z\rfloor )+1)$ alongside a very rough half sine wave approximation (in orange) $$\Gamma ((z-\lfloor z\rfloor )+1)\approx1-\left(1-\frac{\sqrt{\pi }}{2}\right) \sin (\pi (z-\lfloor z\rfloor ))$$

Finally a comparison between the approximate inverse Gamma Function using the half sine wave approximation and the real one