Do isomorphic groups share a binary operation?

Question

Suppose you have two isomorphic groups. Does the binary operation defined on each group need to be the same operation?

Answer 1

Consider this:

$\log: (\mathbb R^+,\times) \to (\mathbb R,+)$ is a group isomorphism.

Answer 2

Not necessarily, no.

The two binary operations behave the same on the underlying sets with respect to the axioms of group theory, yeah, and that's by the fact that the two groups are isomorphic as groups, but it might so happen that, say, one binary operation is the restriction of some bigger relation whereas the other is not.

For example, $(\Bbb Z_3, +_3)\cong H$, where $H=(X, \circ')$, for $X=\{\operatorname{id}, \sigma^2, \sigma^4\}$, is the subgroup of the group $(\{\sigma^i\mid i\in\overline{0,5}\}, \circ)$ of the rotational symmetries of this shape:

,

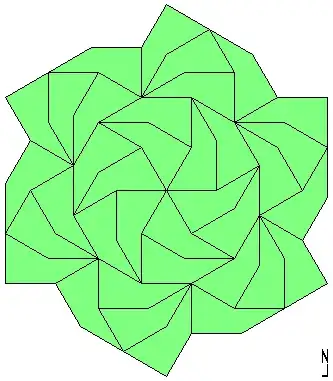where $\sigma$ is a clockwise rotation of $\pi/3$ radians about the centre, so that $\circ'=\circ\rvert_{X\times X}$ is distinct from addition $+_3$ modulo $3$.

Note that here we have simply declared that $\circ'$ is some restriction but $+_3$ is not (although it can be seen as such); also, $\circ'$ is composition of functions, whereas $+_3$ is an arithmetical operation.

---

The underlying sets can be completely different too (as illustrated above). A bijection between sets is not necessarily an equality; think: permutations.

---

Image source.

Answer 3

$G_1 = \{0\}$ and $G_2 = \{1\}$ are groups (each with multiplication as the binary operation).

They are isomorphic, as you can show.

The binary operation of $G_1$ has as its domain $\{(0,0)\}$, while the binary operation of $G_2$ has as its domain $\{(1,1)\}$, so their binary operations are not equal.

Answer 4

To add yet another example to those above, note that if $\mathcal{P}_n$ denotes the group of $n$-by-$n$ permutation matrices (binary operation is matrix multiplication) and $S_n$ denotes the symmetric group (binary operation is function-composition), then these groups are isomorphic via the isomorphism $\sigma \longmapsto P_\sigma$.