How to perfectly split a bezier curve into two curves of unequal length

Question

I couldn't find a title that didn't seem duplicate, but my question is very different from every other I could find on this site.

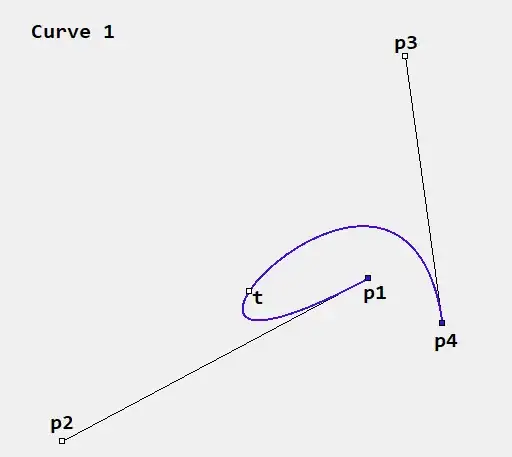
I have a Bezier curve, defined by 4 points. Two of those points (first and last) are "real", and the other two are control points. This is all happening in 2D space. Let's call those points p1, p2, p3 and p4.

I have a fifth 2D point, let's call it t, which is garanteed to be on the curve itself, or at least close enough for all intent and purposes. t can be anything as long as it touches the curve.

What I am trying to do is split this curve into two curves, which would be linked together at point t, and when drawn together, would be exactly the same as the original curve

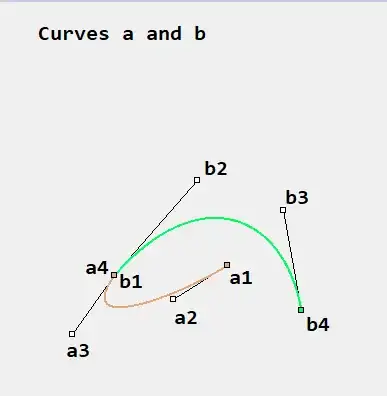
Let's call those two curves a and b, with points a1, a2, a3, a4, b1, b2, b3, b4.

Please forgive the slight differences, this was done in paint. I want perfect equivalency in the final result.

Now, a few of the components of the answer are obvious.

a1 = p1
a4 = b1 = t
b4 = p4

What I am having trouble with, specifically, is finding a2, a3, b2 and b3.

What I did so far

I have figured out that the line segments a3-t and t-b2 should be perfectly parallel, and should be tangent to the curve at point t. I could not figure out how to get this tangent, nor how to determine the length of those segments, so I can't pinpoint the exact location of a3 and b2.

I could figure out how to get the tangent at a point, provided I know exactly how far along the curve my point is (u = [0,1], 0 being right at the start, 0.5 in the middle, etc), thanks to this page. I was unfortunately unable to figure out this value u from my point t.

I could also figure out that the segment a1-a2 should be perfectly parallel to p1-p2 (same goes for b3-b4 and p3-p4). I was not able to figure out how to determine the length of this segment.

I also noticed that all control points, to get the same results, are much closer to the curves after the split than they were before. This seems to suggest that the length of the control segments are somehow determined by a relation between the length of the original control segments and u, since u is always lower than 1 (unless i split on the very end of the curve). In my example, it is obvious that u < 0.5, and the control segments of a are smaller than those of b.

So with everything I know right now, I am confident that I could get my answer to the question if somebody could explain those points:

1. How to find u (distance [0,1] where t is along the curve) from my parameters.
2. How to find the lengths of a3-a4 and b1-b2. (probably related to u)
3. How to find the lengths of a1-a2 and b3-b4. (probably related to u)

Answer 1

The page you link discusses de Casteljau evaluation of a Bézier curve. A further page on the same site explains how this extends to de Casteljau subdivision. This allows you to split the curve into two curves at an arbitrary parameter value, so your second and third points become unnecessary, leaving just the first one:

How to find u (distance [0,1] where t is along the curve) from my parameters.

In fact, de Casteljau subdivision (combined with the convex hull property) is the simple robust way to do just about anything with Bézier curves. Split the curve into two, say at $u = 0.5$. Use the convex hull property to bound the distance between your point $t$ and the two curves. (The distance between $t$ and the nearer endpoint gives an upper bound; the distance between $t$ and the nearer edge of the convex hull gives a lower bound). Discard any curves whose lower bound is greater than the upper bound of a different curve. Split all remaining curves and repeat until the parameter range remaining is small enough.