I'm trying to learn how to express a square root as continued fraction, but I can't get one thing.
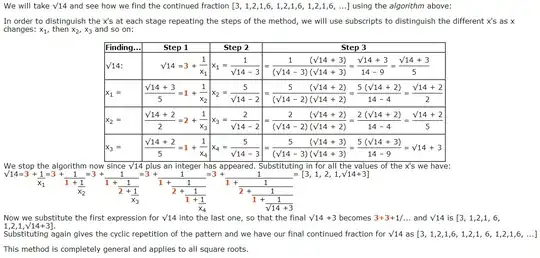
The following example of $\sqrt{14}$ is from this page (click the image to see it at full size):
In the 2nd row of the table, can anyone please tell me where the 1 (in red) comes from? For instance, why can't it be 2, or 3, or 4?
This is my only doubt, which I've been trying hard to understand, but unable to.