2

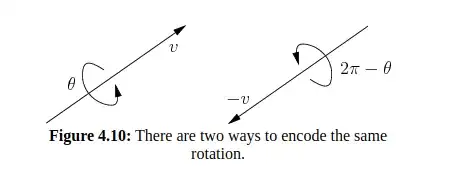
I am given the following question: I need to prove that two quaternions map to the same Rotation Matrix in SO3 Space. It is demonstrated by this image:

enter image description here

Let w be v here. I tried to work out the proof, but it isn't coming out correctly:

$Q=(cos\frac{\theta}{2},w.sin\frac{\theta}{2})$

$Q=cos\frac{\theta}{2}+w_{1}.sin\frac{\theta}{2}.\mathbf{i}+w_{2}.sin\frac{\theta}{2}.\mathbf{j}+w_{3}.sin\frac{\theta}{2}.\mathbf{k}$

As per image, replace $\theta$ with $2\pi-\theta$ and w with -w

$Q=cos\frac{2\pi-\theta}{2}+-w_{1}.sin\frac{2\pi-\theta}{2}.\mathbf{i}+-w_{2}.sin\frac{2\pi-\theta}{2}.\mathbf{j}+-w_{3}.sin\frac{2\pi-\theta}{2}.\mathbf{k}$

$Q=-cos\frac{\theta}{2}+w_{1}.sin\frac{\theta}{2}.\mathbf{i}+w_{2}.sin\frac{\theta}{2}.\mathbf{j}+w_{3}.sin\frac{\theta}{2}.\mathbf{k}$

It is not equal! I am left with $-cos\frac{\theta}{2}$ which is not matching. Please tell me how to fix this

user1436508
  • 376

1 Answers1

2

Since $\sin(\pi-\theta/2)$ equals $\sin(\theta/2)$, not $-\sin(\theta/2)$, you're missing minus signs.

Note $\cos(\theta/2)+\sin(\theta/2)\mathbf{w}$ is expressible as $Q=\exp(\frac{1}{2}\theta\mathbf{w})$ (assuming $\|\mathbf{w}\|=1$).

Replacing $\theta\mapsto2\pi-\theta$ and $\mathbf{w}\mapsto -\mathbf{w}$ yields ${\bf\color{Red}{-}}Q$, not $Q$; you shouldn't be expecting the original quaternion in the first place. Both unit quaternions $Q$ and $-Q$ represent the same 3D rotation.

anon
  • 151,657
  • youre right, so now I get -Q. But how do i actually show that Q and -Q represent the same rotation. i guess physically it works and i can visualize, but how to show mathematically – user1436508 Jan 29 '19 at 16:39
  • Do you know how quaternions are used to represent 3D rotations? Given a quaternion $q$, with polar form $q=\exp(\frac{1}{2}\theta{\bf w})$, and a 3D vector $\bf x$ (in other words, a purely imaginary quaternion), the conjugation $q{\bf x}q^{-1}$ has the effect of rotating $\bf x$ around $\bf w$ by the angle $\theta$. Since $q{\bf x}q^{-1}=(-q){\bf x}(-q)^{-1}$ for all $\bf x$, we conclude $q$ and $-q$ represent the same 3D rotation. – anon Jan 31 '19 at 02:41