8

I'm asked to evaluate the integral $\displaystyle\int_0^\infty \frac{\sqrt{x}\cos(\ln(x))}{x^2+1}\,dx$.

I tried defining a funcion $f(z)=\frac{e^{(1/2+i)\operatorname{Log}(z)}}{z^2+1}$, taking $\operatorname{Log}$ with a branch cut along the positive real axis: ($\operatorname{Log}(z)=\ln(|z|)+i\arg(z))$.

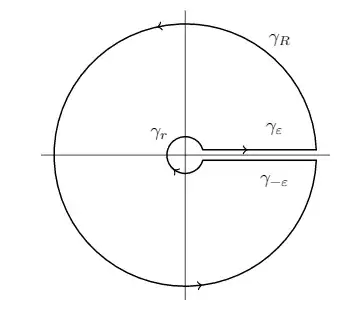
Using residue theorem with the "pacman" contour.

However when trying to bound the integral around a small circle around $0$, I cannot conclude it converges to $0$.

My attempt was $|\int_{\gamma_\epsilon}f|\leq 2\pi\epsilon|e^{(0.5+i)(\ln|\epsilon|+i\theta))}|\frac{1}{\epsilon^2-1}\leq C\epsilon^{-0.5}.$

I'd love it if someone could either suggest a different way to bound the integral around $0$ of this function, or maybe suggest an easier complex function to work with.

Edit:

The wonderful "Related" algorithm of this site managed to link me to this answer Looking at it , a more general statement is proved, but the proof fails when we have $\alpha=0.5+i$ (The circle around $0$ doesn`t converge to $0$ by the proof given there, as a matter of fact any $\alpha$ with $Re(\alpha)>0$ would fail.)

Sar
  • 907
  • Are you forced to use complex analysis? – Frank W Jan 25 '19 at 18:24
  • It's a practice problem for the residue theorem but I`d like seeing different approaches aswell! – Sar Jan 25 '19 at 18:27
  • 1
    I could be wrong, but I doubt you want the branch cut directly on the path of integration! Usually, in complex analysis, you choose branch cuts to avoid the contour altogether. – Adrian Keister Jan 25 '19 at 18:29
  • You`re correct, using a contour of upper half circle with a branch cut along the negative imaginary axis would be more simple, but both yield the same result eventually (And both have the same problem of convergence around 0 ) – Sar Jan 25 '19 at 19:07
  • I tried to evaluate your integral using a different approach without using contour integration (see here) but got stuck on an infinite sum. – omegadot Jan 26 '19 at 10:20

2 Answers2

5

As @Adrian suggested, define $\log z =\log |z|+i\arg(z)$ where $\arg(z)\in (0,2\pi)$ and let the contour be a keyhole contour.
enter image description here

Then $$ \left|\int_{\gamma_R}\frac{e^{(1/2+i)\log z}}{z^2+1}\,dz\right|\le \int_{\gamma_R}\frac{e^{1/2 \log|z|-\arg(z)}}{R^2-1}\,|dz|\le C\frac{R^{3/2}}{R^2-1}\stackrel{R\to\infty}\longrightarrow 0, $$ $$ \left|\int_{\gamma_r}\frac{e^{(1/2+i)\log z}}{z^2+1}\,dz\right|\le \int_{\gamma_r}\frac{e^{1/2 \log|z|-\arg(z)}}{1-r^2}\,|dz|\le Cr^{3/2}\stackrel{r\to 0}\longrightarrow 0. $$ Thus it follows by residue theorem $$ \lim_{\epsilon\to 0}\left(\int_{\gamma_\epsilon} f(z)dz +\int_{\gamma_{-\epsilon}} f(z)dz\right) =2\pi i\left(\text{res}_{z=i}f(z)+\text{res}_{z=-i}f(z)\right). $$ We find$$ \lim_{\epsilon\to 0}\int_{\gamma_\epsilon} f(z)dz=\int_0^\infty \frac{\sqrt{x}e^{i\ln x}}{x^2+1}\,dx, $$ $$ \lim_{\epsilon\to 0}\int_{\gamma_{-\epsilon}} f(z)dz=-\int_0^\infty \frac{e^{(1/2+i)(\ln x+2\pi i)}}{x^2+1}\,dx=+e^{-2\pi}\int_0^\infty \frac{\sqrt{x}e^{i\ln x}}{x^2+1}\,dx. $$ And also $$ \text{res}_{z=i}f(z)=\frac{e^{(1/2+i)\frac{\pi i}{2}}}{2i}=\frac{e^{-\pi/2+\pi i/4}}{2i}, $$ $$ \text{res}_{z=-i}f(z)=-\frac{e^{(1/2+i)\frac{3\pi i}{2}}}{2i}=-\frac{e^{-3\pi/2+3\pi i/4}}{2i}. $$ Thus the given integral is $$ \frac{\pi}{1+e^{-2\pi}}\Re\left(e^{-\pi/2+\pi i/4}-e^{-3\pi/2+3\pi i/4}\right)=\frac{\pi\cosh(\frac{\pi}{2})}{\sqrt{2}\cosh(\pi)}\sim 0.4805. $$ (I found that this value coincides with the integral numerically by wolframalpha.)

Community
  • 1
Myunghyun Song
  • 21,723
  • 2
  • 24
  • 60
  • 1
    This is exactly what I meant to do. Can you please elaborate how you bounded $\gamma_r$ ?( For the small $r$) In addition - I think the factor outside the integral of $\gamma_{-\epsilon}$ is supposed to be $e^{2\pi i(\frac{1}{2}+i)}$ – Sar Jan 25 '19 at 19:29
  • 1
    @Sar Since $r\to 0$, the term $1/(1-r^2)$ is bounded as $r\to 0$. And similarly, since $\arg(z)$ is bounded, $e^{\log|z|/2 -\arg(z)}$ is bounded by $Ce^{\log r/2}=C\sqrt{r}$. Finally, length of $\gamma_r$ is about $2\pi r$. This gives the bound $Cr^{3/2}$. I hope this makes it clear :) – Myunghyun Song Jan 25 '19 at 19:32
  • Yes, Much simpler than I thought . Thank you very much ! Is it true what I commented on the factor on the previous comment? Or am I missing something here? – Sar Jan 25 '19 at 19:35
  • 1
    @Sar Oh, you are also right. Since $e^{2\pi i(1/2+i)}=e^{\pi i-2\pi}=-e^{-2\pi}$, both results are correct. – Myunghyun Song Jan 25 '19 at 19:37
4

Integrating by parts twice, we get $$ \int_0^\infty\cos(x)\,e^{-ax}\,\mathrm{d}x=\frac{a}{a^2+1}\tag1 $$ Therefore, $$ \begin{align} \int_0^\infty\frac{\sqrt{x}\cos(\log(x))}{x^2+1}\,\mathrm{d}x &=\int_{-\infty}^\infty\frac{\cos(x)}{e^{2x}+1}e^{3x/2}\,\mathrm{d}x\tag2\\ &=\int_{-\infty}^\infty\frac{\cos(x)}{e^{2x}+1}e^{x/2}\,\mathrm{d}x\tag3\\ &=\int_0^\infty\frac{\cos(x)}{e^x+e^{-x}}\left(e^{x/2}+e^{-x/2}\right)\mathrm{d}x\tag4\\ &=\int_0^\infty\cos(x)\sum_{k=0}^\infty(-1)^k\left(e^{-(4k+1)x/2}+e^{-(4k+3)x/2}\right)\mathrm{d}x\tag5\\ &=\frac12\sum_{k=0}^\infty(-1)^k\left[\frac{k+\frac14}{\left(k+\frac14\right)^2+\frac14}+\frac{k+\frac34}{\left(k+\frac34\right)^2+\frac14}\right]\tag6\\[6pt] &=\frac\pi{\sqrt2}\frac{\cosh(\pi/2)}{\cosh(\pi)}\tag7 \end{align} $$ Explanation:
$(2)$: substitute $x\mapsto e^x$
$(3)$: substitute $x\mapsto-x$
$(4)$: average $(2)$ and $(3)$ and apply symmetry
$(5)$: expand into power series
$(6)$: apply $(1)$
$(7)$: use $(7)$ from this answer

robjohn
  • 345,667