Probability machine 1 is the first to fail

Question

We are given two machines call them $M1$ and $M2$. $M2$ will be put in use at a time $t$ from now. The lifetime of machine $i$ is exponential with rate $\alpha_i$ $i=1,2$. What is the probability that $M1$ is the first to fail?

Attempt

Clearly, I need to find $P(T_1 < T_2)$ if we call $T_i$ the lifetime of machine $i$.

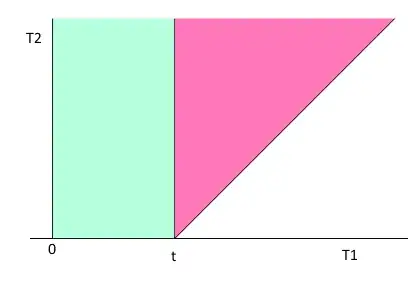
If we consider the time now to be $0$, then we observe that $T_1$ range is $[0,\infty)$ while $T_2$ range is $[t, \infty)$. Therefore, after drawing our sample space in the plane, we see that the required probability is

$$ \int_0^t \int_t^{\infty} \alpha_1 \alpha_2 e^{t (\alpha_1+\alpha_2) } dt_2 dt_1 + \int_t^{\infty} \int_{t_1}^{\infty} \alpha_1 \alpha_2 e^{t (\alpha_1+\alpha_2) } dt_2 dt_1$$

Is my solution correct?

Answer 1

Your solution has several errors.

• The exponents should be negative
• The integration variables, in the exponents, should be $t_1$ and $t_2$ (not $t$!)
• The ranges for the integrals are not right.

Let $E$ be the event of interest. There are two possibilities: $M_1$ fails before time $t$ or after it. Then the probability is

$$\begin{align} P(E) &= P(E \cap T_1 \le t ) + P(E \cap T_1 > t )\\ &= P(E \mid T_1 \le t ) P (T_1 \le t ) + P(T_1 <T_2+t \cap T_1 > t ) \end{align}$$

Now, $P(E \mid T_1 \le t )=1$ (I understand that the event "M1 is the first to fail" include the case where $M_1$ fails before $M_2$ starts!). And $P (T_1 \le t )=\int_0^t \alpha_1 e^{-x\alpha_1}dx $.

Further $$ \begin{align} P(T_1 < T_2+t \cap T_1 > t ) &= P(t < T_1<T_2 + t) \\ &= \int_0^{\infty} \int_{t}^{t_2+t} \alpha_1 \alpha_2 \,e^{-t_1 \alpha_1} e^{-t_2 \alpha_2} dt_1 dt_2 \end{align} $$

Alternatively, you can graph the apt zone, in the $T_1,T_2$ plane. Here the light green corresponds to the first possibility, the pink to the other one. Hence one can readily write

$$P(E) = \int_0^\infty \int_0^t f(t_1,t_2) dt_1 dt_2 + \int_0^{\infty} \int_{t}^{t_2+t}f(t_1,t_2) dt_1 dt_2 $$ Or $$ \int_0^t f(t_1) dt_1 + \int_{t}^{\infty} \int_{t_1-t}^{\infty} f(t_1,t_2) dt_2 dt_1 $$

Answer 2

Look at this post:

pdf of the difference of two exponentially distributed random variables

Your problem is to find the probability that the difference is bigger than $t$.