2

Couple of days back I asked this question. And after reading comments and answer there, even though I knew the definitions of the different terms (tautology, contradiction, contingent, satisfiable, unsatisfiable, valid and invalid) involved, I was quick to realize that I dont know a lot of subtleties, especially connection between these terms. I didnt find one place discussing all these connections. So I spent some time reading comments and answers on that and other linked post and come up with some understanding which I have put below and want your confirmation for it.

First some quick definitions (you may skip this as this super basic. I have put it to avoid any possible ambiguity):

  • Tautology[1]: a formula that is true in every possible interpretation
  • Contradiction: a formula that is false in every possible interpretation
  • Satisifiable[1]: a formula that is true under at least one interpretation
  • Unsatisfiable: a formula is unsatisifable if it is contradiction
  • Valid[2]: a formula is valid if and only if it is true under every interpretation
  • Invalid: a formula is that is false under at least one interpretation

Doubt

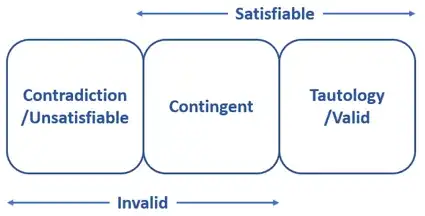
Now to get hold of the connection between all these terms. I prepared below figure:

enter image description here

Next as stated in this comment, "Not a typeX" has two meanings: (1) "The negation of a typeX" and "Not a statement that can be categorized as a typeX".

So, with this in mind, I came up with following relations:

  1. $¬$ tautology $=$ $¬$ valid $=$ contradiction $=$ unsatisfiable
  2. $¬$ contradiction $=$ $¬$ unsatisfiable $=$ tautology $=$ valid
  3. Not a tautology $=$ not a valid $=$ invalid $=$ can be either contradiction or contingent
  4. Not a contradiction $=$ not an unsatisfiable $=$ satisfiable $=$ can be either tautology or contingent
  5. (contradiction $=$ unsatisfiable) $≠$ $¬$ satisfiable $=$ invalid $=$ can be contradiction or contingent
  6. (tautology $=$ valid) $≠$ $¬$ invalid $=$ satisfiable $=$ can be tautology or contingent
  7. Not an invalid $=$ valid $=$ tautology
  8. Not a satisfiable $=$ unsatisfiable $=$ contradiction

Above,

  • $\neg$ means "negation" (or I dont know if it will be more correct or will add more sense if I say a "Boolean negation")
  • "Not a TypeX" means statement "cannot be categorized as TypeX"
  • $=$ simply means "is"
  • $\neq$ simply means "is not"

I know these are pretty much basic stuff but was source of a lot of confusion for me and I wanted all these related things noted down at one place in correct way. Can anyone confirm if above bullet points and figure are correct?

ryang
  • 38,879
  • 14
  • 81
  • 179
RajS
  • 1,317

1 Answers1

2

Long comment

Consider first the negation of the definition of tautology :

A formula $\varphi$ is a tautology iff is true in every possible interpretation.

We can re-write it as follows : for every interpretation $\mathfrak I$, the formula $\varphi$ is true.

Thus, its negation is : there is an interpretation $\mathfrak I_0$ such that the formula $\varphi$ is not true, i.e. false.

But, to say that the formula is false for some interpretation does not imply that it is false for every interpretation.

Conclusion :

a formula that is not a tautology can be either unsatisfiable or satisfiable.

Different is the case with the negation of a formula $\varphi$.

If $\varphi$ is a tautology, then it is true for every interpretation.

Thus, its negation $\lnot \varphi$ is false for every interpretation.

Conclusion :

if $\varphi$ is a tautology, then $\lnot \varphi$ is unsatisfiable, i.e. a contradiction.

In this way, we have covered all cases :

tautology (aka : valid), unsatisfiable (aka : contradiction), satisfiable.

Mauro ALLEGRANZA
  • 94,169
  • I believe your first conclusion is my point 3 in doubt section of question. The only thing I missed to state "explicitly" in point 3 is that it can also be satisfiable (even thought I have specified contingent in point 3, which is also satisfiable). Same is case with your conclusion 2, which I feel is exactly same as my point 1 in doubt section of question. Right? – RajS Jan 21 '19 at 12:17
  • @anir - contingent is an "old" term : "neither true under every possible valuation (i.e. tautology) nor false under every possible valuation (i.e. contradiction)." Thus, according to this def, a contingent proposition cannot be a contradiction, and thus cannot be unsatisfiable. – Mauro ALLEGRANZA Jan 21 '19 at 12:31
  • Regarding your points, the gist of my long comemnt is : it is not necessary (and it can be misleading) to consider all the above cases, when we have only three basic terms in place : tautology/satisfiable/ contradiction. Then we can easily apply them to a formula starting with a negation sign. – Mauro ALLEGRANZA Jan 21 '19 at 12:34
  • Hi Mauro, sorry to grab your attention like this. I needed to know exhaustively how all terms relate to each other, especially because those terms are used in exams. Thats why I also included contingent, valid and invalid in the discussion. I have edited new question to put all relations I can think of exhaustively. Can you please have a look at it and reopen the question if appropriate. 4 people have already voted to reopen. – RajS Sep 09 '19 at 06:10