It’s a bit easier to tease out the geometry if you switch to homogeneous coordinates† and express the transformation as a matrix product: $$\mathbf x' = H\mathbf x = \begin{bmatrix}e_1&f_1&g_1\\e_2&f_2&g_2\\e_0&f_0&g_0\end{bmatrix} \begin{bmatrix}x\\y\\1\end{bmatrix}.$$ Recalling that the columns of a transformation matrix are the images of the basis vectors, we can see immediately that $H$ maps the source image coordinate origin to the destination image point $(g_1/g_0,g_2/g_0)$ (assuming that $g_0\ne0$, that is). The first column is the image of $(1,0,0)^T$, so assuming that the $x$- and $y$-axes are horizontal and vertical in the source image, $v_x=(e_1/e_0, e_2/e_0)$ is the vanishing point in the destination of horizontal lines in the source. That is, horizontal lines in the source image are mapped to lines that converge at $v_x$. If $e_0=0$, then $v_x$ is a point at infinity, so $H$ maps parallel horizontal lines to parallel lines, though they will now be parallel to the vector $(e_1,e_2)$ instead of horizontal. Similarly, the second column of $H$ is the vanishing point $v_y$ of vertical lines in the source image. So, for instance, if you map the square $[-1,1]\times[-1,1]$ in the source to the quadrilateral $ABCD$ in the illustration below, a rectangular grid on that square will end up looking like the one in the illustration.
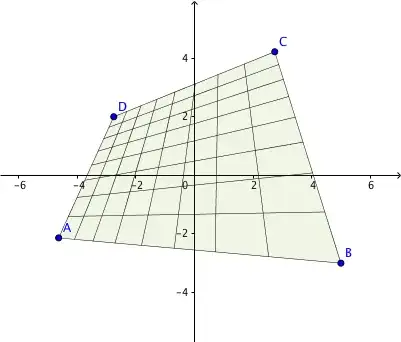
This is also the image that you might get after taking a picture of the ruled square at an oblique angle with a pinhole camera.
Notice how the ends of the grid lines are not evenly spaced in the image. Projective transformations preserve cross-ratios of points on a line, and since the horizontal and vertical vanishing points in the destination image are finite (they are, respectively, the intersections of lines $AB$ with $DC$ and of $AD$ with $BC$) the spacing between adjacent pairs of grid lines is no longer uniform. This is the same phenomenon that you see in photos of fences or railroad tracks that recede into the distance: as the fence/tracks get farther from the camera, the posts/ties appear to get closer and closer together.
Typically, you might construct this homography between two images by matching some convex quadrilateral, not necessarily a square or rectangle, in one image to a convex quad in the other. There’s a nice explanation of how to construct the matrix $H$ given the two quads here. However, there’s another way to understand the mapping that might be more illuminating.
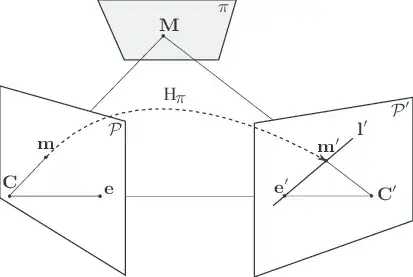
Imagine the two images lying on a pair of planes embedded in the three-dimensional scene. You can then map the first image onto the second by back-projecting it onto some third transfer plane in the scene, and then projecting from that onto the second image plane. There is extensive literature on the mathematical relationships between pairs of images of the same scene. Look up epipolar geometry as a starting point.
† I’m not going to give more than a cursory definition, if any, of basic terms that are easily looked up on the Internet.


