3

A cone has its guiding curve to the circle $x^2+y^2+2ax+2by=0$ and passes through a fixed point $(0,0,c)$. If the section of the cone by plane $y=0$ is a rectangular hyperbola. Prove that the vertex lies on fixed circle $x^2+y^2+z^2+2ax+2by=0$ and $2ax+2by+cz=0$.

Attempt:

Using equation of circle and fixed point, equation of cone can be found out, it comes:

$$cx^2+cy^2-2axz-2byz+2acx+2bcy=0$$

Its section by $y=0$ plane comes out to be $$cx^2-2axz+2ax=0$$

I am unable to proceed further. Please help

Intelligenti pauca
  • 50,470
  • 4
  • 42
  • 77
Sanchit Vijay
  • 33
  • Your equation for the cone cannot be right: it contains all the $z$-axis and not only point $(0,0,c)$. – Intelligenti pauca Jan 20 '19 at 18:31
  • @Aretino since z axis is also one of the generating line. As it passes through origin and (0,0,c). Therefore equation of cone contain all the z axis. – Sanchit Vijay Jan 22 '19 at 07:57
  • 1
    It needn't be so: if the $z$-axis were a generatrix then the vertex of the cone would lie on the $z$-axis, contradicting the claim that it belongs to a circle. Point $P=(0,0,c)$ can lie on the cone even if $z$-axis is not a generatrix: just join $P$ with any point $Q$ on the guiding circle (different from the origin) and choose cone vertex at will on line $PQ$. – Intelligenti pauca Jan 22 '19 at 11:51
  • I think there is a misunderstanding. What i interpreted from the question is that we need to find vertex of hyperbola. Because P(0,0,c) is the fixed point so each generatrix must pass through it and therefore it is a vertex. – Sanchit Vijay Jan 23 '19 at 06:03
  • The vertex of the hyperbola, as the hyperbola itself, lies on plane $y=0$, while the circle given as solution lies on a different plane. Hence I'm afraid your interpretation doesn't hold. In my opinion the locus is formed by the vertex of the cone. – Intelligenti pauca Jan 23 '19 at 13:39
  • Moreover, the intersection between your cone and plane $y=0$ is a couple of lines, not a hyperbola. – Intelligenti pauca Jan 23 '19 at 14:27

2 Answers2

2

Let $V=(x_0,y_0,z_0)$ be the vertex of the cone. The cone is composed of all lines passing through $V$ and a point of circle $\gamma$ of equation $x^2+y^2+2ax+2by=0$ in the $xy$ plane; the equation of the cone is then: $$ (z_0x-x_0z)^2+(z_0y-y_0z)^2+2a(z_0x-x_0z)(z_0-z)+2b(z_0y-y_0z)(z_0-z)=0. $$ Intersecting this with plane $y=0$ gives the equation of a conic in the $xz$ plane: $$ (z_0x-x_0z)^2+y_0^2z^2+2a(z_0x-x_0z)(z_0-z)-2by_0z(z_0-z)=0. $$ This represents a rectangular hyperbola if the coefficients of $x^2$ and $z^2$ in that equation are opposite, which leads to the equation: $$ \tag{1} x_0^2+y_0^2+z_0^2+2ax_0+2by_0=0. $$ This is the equation of the sphere having $\gamma$ as a great circle.

We know, on the other hand, that point $P=(0,0,c)$ lies on the cone, implying that $V$ belongs to the cone having $P$ as vertex and $\gamma$ as guiding curve. Hence the coordinates of $V$ must satisfy the equation: $$ \tag{2} cx_0^2+cy_0^2+2ax_0(c-z_0)+2by_0(c-z_0)=0. $$ Combining equations $(1)$ and $(2)$ we obtain the equation of a plane, to which $V$ must then belong: $$ \tag{3} 2ax_0+2by_0+cz_0=0. $$ Vertex $V$ must then lie on the intersection of sphere $(1)$ and plane $(3)$, which is exactly the circle we were required to find.

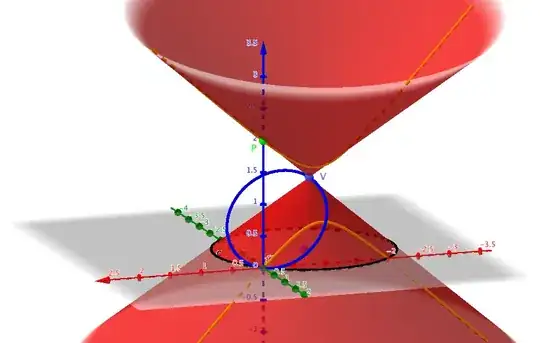
enter image description here

Intelligenti pauca
  • 50,470
  • 4
  • 42
  • 77
  • how did you write the equation of cone , i am not aware of this method. – ashishyadaveee11 Dec 26 '19 at 11:10
  • 1
    @ashishyadaveee11 See here: https://math.stackexchange.com/a/183690/255730 – Intelligenti pauca Dec 26 '19 at 22:53
  • @ashishyadaveee11 Or, even better, here: http://www.mndcollegerajur.org/uploads/department/cone.pdf – Intelligenti pauca Dec 28 '19 at 20:50
  • I think the pdf has misprint while homogenising with z equation, (-0) should come instead. – ashishyadaveee11 Dec 29 '19 at 05:17
  • @Intelligentipauca , Can you please elaborate and generalize this statement --'This represents a rectangular hyperbola if the coefficients of $^2 $and $^2$ in that equation are opposite' – llecxe Jan 05 '21 at 15:02
  • @HarshVardhanSingh See here: https://en.wikipedia.org/wiki/Hyperbola#Quadratic_equation where it gives the formulas for $a$ and $b$, which must be the same in the case of a rectangular hyperbola. Other explanations are also possible. – Intelligenti pauca Jan 05 '21 at 15:14
  • @Intelligentipauca , Sir , can we generalize this and say that if the equation of a rectangular hyperbola in the xy plane is given by $Ax^2 + By^2 +Cxy + D=0$ , then it represents a rectangular hyperbola iff $A+B=0$ – llecxe Jan 05 '21 at 15:22
  • @HarshVardhanSingh Yes, of course. And the same is true for the more general equation $Ax^2+By^2+Cxy+Dx+Ey+F=0$. – Intelligenti pauca Jan 05 '21 at 16:20
  • @Intelligentipauca Thanks for replying and answering my query. – llecxe Jan 05 '21 at 16:22
0

That the guiding curve is a circle implies that the axis of the cone is perpendicular to the plane of the circle (that is, the $xy$-plane, which we'll call "the horizontal") and passes through the circle's center, $(-a,-b,0)$.

Also, it is "known" (and shown in this answer) that the eccentricity of a conic is given by $$e = \frac{\sin \angle P}{\sin \angle C} \tag{1}$$ where $\angle C$ and $\angle P$ are the "cone angle" and "plane angle", the angles with the horizontal made by the cone's generator-lines and the cutting plane, respectively. Now, a rectangular hyperbola has eccentricity $\sqrt{2}$, and the plane $y=0$ makes $\angle P = 90^\circ$ with the horizontal; we find, then, that $\angle C = 45^\circ$. Consequently, the height of the cone's vertex above (or below) the $xy$-plane must be equal to the guiding circle's radius, $\sqrt{a^2+b^2}$.

The vertex of the cone is thus $$V = (-a,-b,\pm\sqrt{a^2+b^2}) \tag{2}$$ which clearly satisfies the target equation $$x^2 + y^2 + z^2 + 2 a x + 2 b y = 0 \tag{3}$$ for the sphere that has the guiding circle as a great circle.

Note that we have not yet introduced the "fixed point" $C := (0,0,c)$. Since we have deduced the cone's vertex without this point, we find that $c$ is not actually a free parameter in this problem. Indeed, one readily sees that, because $\overline{OV}$ and $\overline{VC}$ are generators making $45^\circ$ angles with the horizontal, $\triangle OVC$ is an isosceles right triangle with apex $V$; necessarily, the $z$-coordinate of $C$ must be twice the $z$-coordinate of $V$: that is, $c = \pm 2 \sqrt{a^2+b^2}$. Thus, the target plane $$2 a x + 2 b y + c = 0 \qquad\to\qquad a x + b y \pm z \sqrt{a^2+b^2} = 0 \tag{4}$$ is easily seen to be satisfied by $V$. $\square$

Blue
  • 75,673