Are the following logical statements all axioms of propositional calculus?

Question

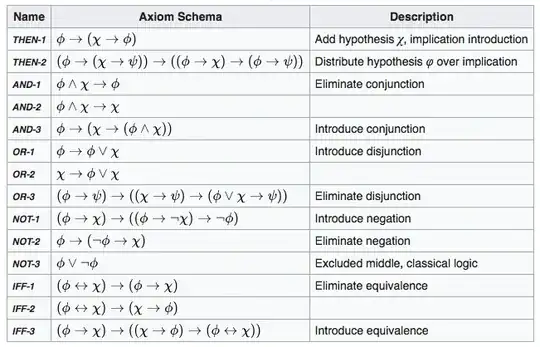
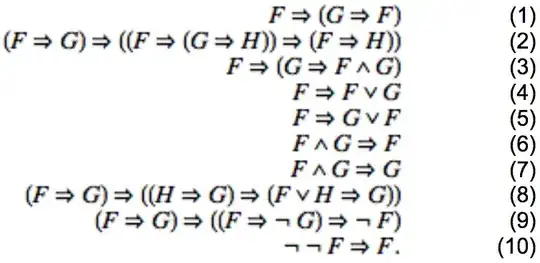I have found conflicting lists of axioms in propositional calculus in Kleene, $2002$, and on Wikipedia. From what I can tell, carefully reasoning through each of the statements reveals that are tautologies, and since the only real understanding I have surroundings logical axioms is that they are tautologies, I can't quite decide which source to trust.

Wikipedia's axioms:

Kleene's axioms:

Any help is appreciated, thank you.

score 1 · Accepted Answer · answered Jan 19 '19 at 12:13

1

There are many different (but equivalent) axiomatizations of propositional calculus. See e.g. List of Hilbert systems.

The fist nine are the same.

Kleene's version does not use the $\Leftrightarrow$ connectives; thus, the last three axioms of Wiki's list are not needed in Kleene's version.

The only real difference regards the axioms fo $\lnot$.

Kleene's axiom 10 is Double Negation elimination : it is equivalent to LEM (axiom not-3).

answered Jan 19 '19 at 12:13

Mauro ALLEGRANZA

94,169

Thank you for the clarification, I had a skim over the cited list; interesting stuff. – joshuaheckroodt Jan 19 '19 at 15:57
@joshuaheckroodt - regarding $\lnot$ and different equivalent sets of rules (or axioms) you can see the answer to this post. – Mauro ALLEGRANZA Jan 19 '19 at 16:36
The way this gets phrased suggested that the above consist of axioms. None of what gets listed though makes for an axiom since none of those are well-formed, and by definition, an axiom has to be well-formed. – Doug Spoonwood Jan 19 '19 at 18:56

score 0 · Answer 2 · answered Jan 19 '19 at 18:55

0

No, what gets listed are not axioms. None of those are well-formed, and thus to call them axioms is not correct. That said, it probably isn't difficult for many who know an appropriate definition of a well-formed formula to write the intended axioms from the symbols given.

answered Jan 19 '19 at 18:55

Doug Spoonwood

11,211

The assumption in both cases is that the symbols that are used to stand in for statements are well-formed. – joshuaheckroodt Jan 19 '19 at 18:58
@joshuaheckroodt If some sequences of symbols A gets used to stand in for a well-formed statement, then A is not well-formed. If B is an axiom, then it it is well-formed. So, A cannot be an axiom without a contradiction. – Doug Spoonwood Jan 19 '19 at 19:09
How does this assumption "Let $\phi$, $\mathcal{X}$, and $\psi$ stand for well-formed formulas. (The well-formed formulas themselves would not contain any Greek letters, but only capital Roman letters, connective operators, and parentheses.) Then the axioms are as follows" aid the composition of axioms, in which case? – joshuaheckroodt Jan 19 '19 at 19:13
@joshuaheckroodt I don't understand what you're asking. – Doug Spoonwood Jan 21 '19 at 04:37

score 0 · Answer 3 · answered Feb 02 '24 at 20:46

There are many equivalent axiomatizations of propositional logic; the one that gets used is up to you. It is possible to prove that a theory is complete by showing that any tautology in the the theory is provable. For all of these axiom systems, their completeness has been proven. Some axiom systems prefer to be incomplete, such as theories which do not accept the law of excluded middle. Different axiom systems have different strengths and weaknesses, depending on what you're trying to prove.

Are the following logical statements all axioms of propositional calculus?

3 Answers3