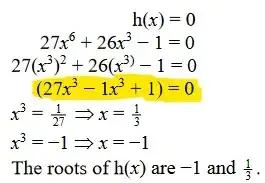Find all real roots of $h(x)$.
I have solved the question by letting $u = x^3$ and then using the quadratic formula to solve $27u^2+26u-1 = 0$.
However I don't have a clue as to how they've achieved $27x^3 -1x^3+1=0$ as one of the steps. I have highlighted the section in the image linked Solution.
It's a typo, it should read
$$ \begin{align}&27(x^3)^2 + 26 x^3 - 1\\ =\ &(27x^3-1)(x^3+1) \end{align}$$
Remark $ $ You could have inferred this from what follows, i.e. they reduce it to
$\,x^3 = 1/27\,$ and $\,x^3 = -1\,$ implying that it has factors $\,27x^3-1\,$ and $\,x^3+1$
Worth mention is that we can use the AC method to factor such polynomials, i.e.
$$\begin{eqnarray} \rm\: a\:f(x)\:\! \,=\,\:\! a\:(a\:x^2 + b\:x + c) &\,=\,&\!\!\rm\: \color{#c00}{X^2} + b\:X + \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\overbrace{ac,}^{\rm\qquad\ \ \ \ \ {\bf\large\ \ AC-method}}}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \ X = a\:x \\ \end{eqnarray}$$ In our case $$ {\begin{eqnarray} f \, &\,=\,& \ \ \, 27 x^2+\ 26\ x\,\ -\ \ 1\\ \Rightarrow\,\ 27f\, &\,=\,&\!\,\ (27x)^2\! +26(27x)-1\\ &\,=\,& \ \ \ \color{#c00}{X^2}+\, 26\ X\,\ -\ 1,\,\ \ X\, =\, 27x\\ &\,=\,& \ \ \ \ (X+27)\ (X-1)\\ &\,=\,& \ (27x+27)\,(27x-1)\\ \Rightarrow\ \ f\:=\: \color{#0a0}{27^{-1}}\,(27f)\, &\,=\,& \ \ \ \ \ \ \ (x+ 1)\ (27x-1)\\ \end{eqnarray}}$$
