Let $X$ be a (connected) topological space with a $C^\infty$ atlas. It is a known theorem that if $X$ is second-countable and Hausdorff, then it admits partitions of unity. I'm trying to prove the "reverse" theorem:
Let $X$ be a (connected) topological space with a $C^\infty$ atlas. If $X$ admits partitions of unity, then $X$ is second-countable and Hausdorff.
I was able to prove the Hausdorff condition by taking a partition of unity $\{\rho_p,\rho_q\}$ subordinate to $\{M-\{p\},M-\{q\}\}$ and taking neighbourhoods $U,V$ of $p,q$ small enough so that the values of $\rho_p,\rho_q$ in $U$ conflict with the ones in $V$ so that $U\cap V=\emptyset$.
Now I'm stuck with second-countability. Here is my attempt:
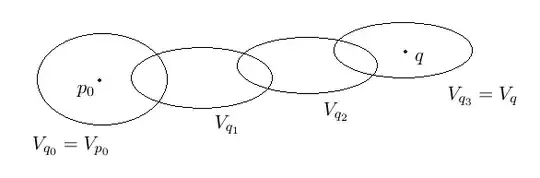
For each $p\in M$ take a chart $\varphi_p:U_p\to\mathbb{R}^n$. For a partition of unity $\{\rho_p\}$ subordinate to $\{U_p\}$, let: $$V_p:=\rho_p^{-1}(0,\infty)\subset U_p$$ By definition of partition of unity, $\{V_p\}$ is a locally finite refinement of $\{U_p\}$. Now since $U_p$ is homeomorphic to $\mathbb{R}^n$, $U_p$ is second countable and therefore $V_p$ is second-countable.
I think the natural thing to do is to find countably many points $\{p_n\}_{n\in\mathbb{N}}$ so that $\{V_{p_n}\}_{n\in\mathbb{N}}$ is a cover for $X$, but I can't see how to do that.