20

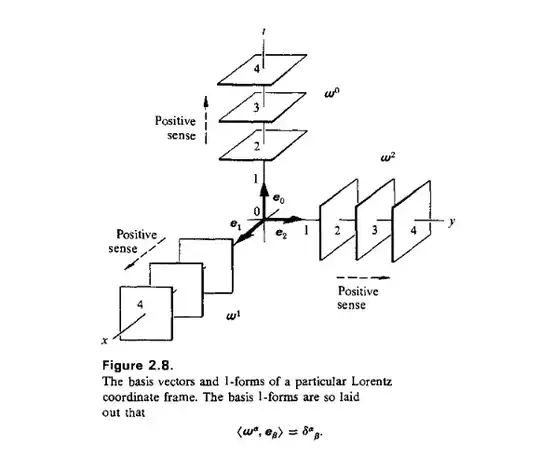
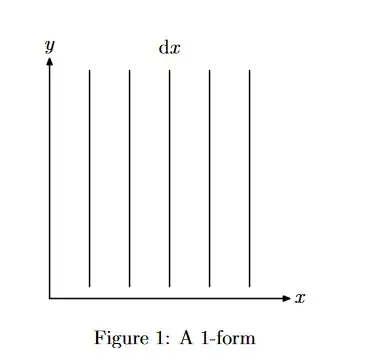
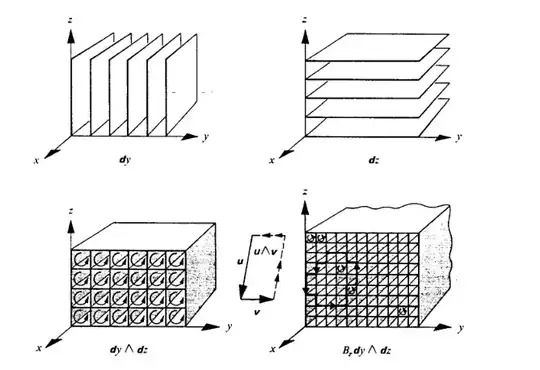
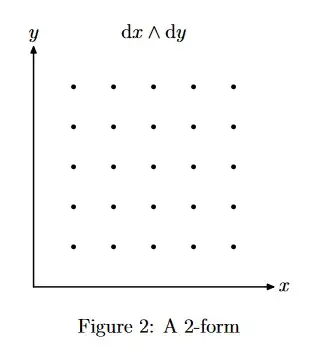
I think I understood 1-forms fairly well with the help of these two sources. They are dual to vectors, so they measure them which can be visualized with planes the vectors pierce.

But I struggle with the explanations for higher order forms.

The goal is to answer and understand these questions with drawings:

  1. How can I visualize the wedge between two 1-forms $\alpha\wedge\beta$? I think I understood the wedge between two vectors, as the parallelogram created by the two in a "area sense". The determinant comes in to make it only about the area which is why $v\wedge w = \frac{1}{2}v\wedge 2w$ since stretching the parallelogram by two in the w direction is compensated by squishing it in the v direction, so the area stays constant. So the wedge between two vectors is the area it spans with its vectors. But how does that translate to the dual space? Where 1-forms measure the length of the component of its dual vector. And can be visualized as planes the vectors pierce through. What is the visualization between two of these 1-forms as a wedge?

Gravitation has this picture:

2-forms Dan-Piponi drew it like this:

2-forms dan

Now these pictures make some sense as they are generated by intersecting the 1-forms. But I am not quite getting how the result is evaluated. The result (2-form) should map two vectors as input to a number. And I don't see how these intersections do that. While for 1-forms you count the numbers of planes a vector pierced.

  1. Why does it make sense that $d(d\alpha)=0$ for every differential form $\alpha$
  2. What does Dan Piponi mean by saying: "exterior derivative is none other than finding the boundary of the picture" (4 Exterior Derivatives)
  3. Understand part 5 about Stokes' theorem from Dan Piponi's paper

Note: I should maybe add that I have no background in physics, so I didn't understand a lot of the stuff in Gravitation. I just tried to read it after I couldn't quite understand other source since it was cited there.

Similar questions:

  • What's the geometrical intuition behind differential forms?

    Edit (since someone voted "close", based on this question as a duplicate): This question indicates not grasping how 1-forms work ("families of surfaces [...] Why do this interpretation makes any sense?") not only does that invite explanations for 1-forms and hand-waving away the rest with "it works similarly in higher dimensions" but it in particular does not mention specific visualizations for 2-forms which kind of show that there should be an intuition for 2-forms (and maybe higher). And while this question accepted an answer already, this answer does not help to answer the (enumerated) questions above. So this is absolutely not a duplicate.

  • Geometric understanding of differential forms.

  • Visualizing Exterior Derivative

Felix B.
  • 2,425
  • 3
    Hi, I drew some pictures to visualize differential forms before, with explanation for $dd\alpha=0$ (but not for wedge products, and different from Dan Piponi's illustrations). I hope these pictures are also helpful to you. https://math.stackexchange.com/a/2750165/266571 – autodavid Jan 20 '19 at 18:00
  • 1
    @autodavid thank you, that explained a lot of my questions, I am just still not getting how to interpret the pictures I posted but I realized (because of your suggestion to view differential forms as functions) that since $<A\wedge B , v\otimes w>= <A\otimes B, v\wedge w>$ I can now view 2-forms as a linear function evaluating parallelograms, so I think you deserve 50 reputation for that. – Felix B. Jan 21 '19 at 20:09
  • 1
    I'm glad that it helps. But I have to say that my explanation for exterior derivative is just an intuition and not a way to calculate $d\alpha$. So the answer is modified to warn this. (It is still a helpful intuition, which comes from singular cohomology). Viewing differential forms as "alternating linear functions" pointwisely is still no problem because it is just the definition of forms. – autodavid Jan 22 '19 at 19:21
  • 1
    Hmm... Is it really true that $\langle A\wedge B , v\otimes w\rangle = \langle A\otimes B, v\wedge w \rangle$ ? I think it should be $\langle A\wedge B , v\otimes w\rangle = \langle A\wedge B, v\wedge w \rangle$. – autodavid Jan 22 '19 at 19:26
  • 1
    $A\wedge B = A\otimes B - B\otimes A $ thus $\langle A\wedge B, v\otimes w\rangle = \langle A\otimes B, v\otimes w\rangle -\langle B\otimes A, v\otimes w\rangle = A(v)B(w)-B(v)A(w) = A(v)B(w) + A(-w)B(v) = A\otimes B (v\otimes w - v\otimes w) = \langle A \otimes B, v\wedge w\rangle $ – Felix B. Jan 22 '19 at 21:49
  • Oh I see, thank you. Our definitions of $v\wedge w$ are different. I use the one in wikipedia so I cannot expand $v\wedge w$ like yours. But our definition of $A\wedge B$ is the same. – autodavid Jan 23 '19 at 08:26
  • It ends up as the same, you just need to show that this natural surjection into the equivalence classes $\pi$ equals this mapping. We defined $A\wedge B := \frac{1}{p!q!}\mathcal{A}^{p+q}(A\otimes B)$ with $\mathcal{A}^{p}(A)=\sum_{\sigma \in S_p} \text{sign}(\sigma)\sigma.A$ where $\frac{1}{p!}A^{p}$ is the identity on elements of $\bigwedge^p V$ and maps elements in the equivalence class of $0$ to zero. Since this mapping is linear it is in fact $\pi$ – Felix B. Jan 23 '19 at 11:39
  • Now that I think about it there might be some funny business with scalars and it might be off a bit, by the factor $\frac{(p+q)!}{p!q!}$ – Felix B. Jan 23 '19 at 11:52
  • I found differential forms difficult to understand at first and did not find these pictures helpful at all. I do call them "measuring instruments". The level sets of a $1$-tensor are evenly spaced parallel hyperplanes. Higher order forms can be viewed as measuring instruments for the area or volume of parallelotopes. But in the long run, what I say is that differential forms provide a powerful algebraic tool for analyzing geometric statements. So once you understand the rules, they're a wonderful way to explore consequences of geometric assumptions, – Deane Jun 07 '21 at 13:19
  • @Deane: I usually consider each $p$-form as an embedded submanifold. Is this interpretation wrong ? – C.F.G Jun 07 '21 at 14:12
  • @Buraian no (see edit) – Felix B. Jun 28 '21 at 07:11
  • @C.F.G, could you explain how you see a $p$-form as an embedded submanifold? One could try to define submanifolds of codimension $p$ as ones on which the $p$-form, when pulled back to each submanifold, vanishes. But such submanifolds don't always exist. – Deane Jun 28 '21 at 14:47
  • On one hand, \begin{align} \langle A\wedge B, v\otimes w\rangle &= \langle A\otimes B - B\otimes A, v\otimes w\rangle\& = \langle A,v\rangle\langle B,w\rangle - \langle A,w\rangle\langle B,v\rangle. \end{align} If you define the wedge product of two vector using the same formula, then \begin{align}\langle A\wedge B, v\wedge w\rangle&= \langle A,v\rangle\langle B,w\rangle - \langle A,w\rangle\langle B,v\rangle - \langle B,v\rangle\langle A,w\rangle + \langle B,w\rangle\langle A,v\rangle\&= 2(\langle A,v\rangle\langle B,w\rangle - \langle A,w\rangle\langle B,v\rangle) \end{align} – Deane Jun 28 '21 at 15:24
  • @Deane: (If I am mistaken please correct me). By De Rham isomorphism between Homology groups and cohomology groups having a $p$-form is same as considering a $p$-cycle. Isn't? – C.F.G Jun 28 '21 at 18:16
  • @C.F.G, for a closed manifold that's correct, but that's a rather deep and difficult theorem, so it doesn't provide much insight into what a diffferential form is. – Deane Jun 29 '21 at 02:55

2 Answers2

3
  1. How can I visualize the wedge between two 1-forms $α∧β$?

First we need to understand what the wedge actually does. In your case it creates a new fully anti-symmetric tensor (think determinant) of order 2. A 2-form is a thing that takes two vectors and returns a scalar. If, for example, we plug a vector into a 1-form we get a number. We also know that forms are multi-linear, therefore we can pull out all the factors and apply the form on each basis-vector individually. So in practice a 1-form just projects a vector and measures the length of that projection. Following this, a 2-form can be visualized as a thing that first takes a vector and becomes a 1-form.

But how does that translate to the dual space? What is the visualization between two of these 1-forms as a wedge?

Let's say we are in $\Lambda(\mathbb{R}^3)$, your 2-vector $a \wedge b$ can be thought of as something with the magnitude of the enclosed parallelogram of $a,b$ and an additional other property - path orientation. These two properties are taken by the 2-form to return a number. You might get the impression that this looks very similar to integration, and you would be right. The way they scale and how they compute vectors is exactly how integration works.

  1. Why does it make sense that $d(d\alpha)=0$ for every differential form $\alpha$

We know that the exterior derivative $d$ takes a (n-1)-form to an n-form. Since a form is also full anti-symmetric we combine that with the Schwarz integrability condition, that the second derivatives are symmetric and arrive at statements like $ \operatorname{div}(\operatorname{rot}a)= 0$ or $\operatorname{rot}(\operatorname{grad}\phi)= 0$. This is just the general statement.

  1. What does Dan Piponi mean by saying: "exterior derivative is none other than finding the boundary of the picture" (4 Exterior Derivatives)

Let us operate in $\Omega (\mathbb{R^3})$ and look at the object \begin{eqnarray} \phi &=& x_1+x_2+x_3\\ d\phi &=& \frac{\partial \phi}{\partial x_1}dx^1+\frac{\partial \phi}{\partial x_2}dx^2+\frac{\partial \phi}{\partial x_3}dx^3\\ d\phi &=& dx^1+dx^2+dx^3\\ \end{eqnarray} Over what boundary do you need to integrate $d\phi$ to retrieve the information of $\phi$?

Michael Paris
  • 741
0

Below, a tensor is an alternating multilinear function on a vector space, and a form is an assignment of a tensor to the tangent space at each point of a manifold.

A finite dimensional vector space can be viewed as a space with an origin and arrows. Even though the dual space is also a vector space, I don't find it useful to view it the same way. Instead, I view a nonzero 1-tensor as a measuring instrument. It defines a way of measuring the spacing between two parallel (affine) hyperplanes in the vector space itself with respect to a unit of distance. An abstract vector space along has no units of distance. A choice of a nonzero 1-tensor defines both the set of parallel hyperplanes, as well as the units used for measuring the spacing.

As for a exterior $2$-tensor ($2$-form) that is decomposable (i.e., it can be written as a wedge product of $1$-tensors), I view it as a way to measure the (oriented) area of a parallelogram defined by two vectors in the space. It captures the fundamental properties of area. One then observes that such tensors can be extended to an abstract vector space. Again, rescaling a $2$-tensor corresponds to changing the units with respect to how the area is measured.

The higher order exterior tensors are similar.

From this point of view, the wedge product is simply a way to take a $k$-form (i.e., a a way to measure the $k$-dimensional volume of a $k$-dimensional parallelotope) and an $l$-form (i.e., a a way to measure the $l$-dimensional volume of a $l$-dimensional parallelotope) and use the two together to measure $(k+l)$-dimensional volumes. This construction satisfies many remarkable properties that are all captured algebraically in the definition of the wedge product and the properties implied by it.

I view the exterior derivative of a differential form to be the "right way" to extend the fundamental theorem of calculus to higher dimensions. If you write the obvious extension of the FTC to a rectangular region in a way that does not favor any particular direction of integration and that captures orientation properly, the formula for exterior differentiation arises naturally. That $d^2 = 0$ indicates that if you apply the fundamental theorem of calculus twice, you get nothing because the boundary of the boundary of a region is empty.

As you can see, I do not try to visualize forms as geometric objects. They are instead practical ways to perform measurements on the geometric objects in the vector space.

Deane
  • 7,582