Probability distribution for smallest angle between 3 lines

Question

I was running a computer simulation to get the distribution of smallest angle between 3 random lines (in $2$D) lying on the unit circle (i.e. lines between the center and the circumference). Explicitly, I draw 3 numbers uniformly in $[0,2\pi]$. I define $v_i = (\cos{\theta_i},\sin{\theta_i})$, and calculate $$ d\theta_1 = \arccos (v_1\cdot v_2) $$ $$ d\theta_2 = \arccos (v_1\cdot v_3) $$ $$ d\theta_3 = \arccos (v_2\cdot v_3) $$ I calculate $\Theta = \min\{d\theta_1,d\theta_2,d\theta_3\}$. I run this a lot of times to get a distribution:

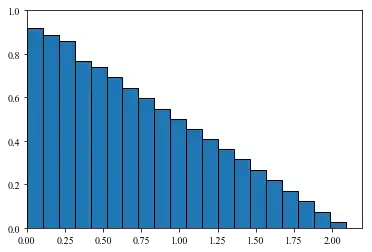
where the $x$-axis is $\Theta$ in radians. I do not know how exactly to calculate this analytically, but even more importantly I look for intuition. This distribution tells us that the most probable result is that two out of three randomly chosen directions will fall on top of each other. This is counter-intuitive for me. My (obviously wrong) intuition tells me that this should peak around (maybe not exactly) the mean, $\frac{\pi}{3}$.

Answer 1

It is a little hard to see, but the probability that $\theta_1$ is less than $\theta_2$ and $\theta_3$ is $\frac{2 \pi - 3 \theta_1}{2 \pi}$. To see this, imagine that $\theta_1\in(0, 2\pi/3)$, $v_1 = (1,0)$, $v_2 = (\cos \theta_1, \sin \theta_1)$, and $v_3=(\cos \alpha, \sin \alpha)$ where $\alpha\in (-\pi, \pi)$. Then the only way that $\theta_1$ can be less that $\min(\theta_2,\theta_3)$ is if $\alpha>2\theta_1$ or $\alpha<-\theta_1$. (Note that $\theta_2 = |\alpha|$).

If you now believe that $$ P(\theta_1 <\min(\theta_2,\theta_3) | \theta_1=\theta) = \frac{2 \pi - 3 \theta}{2 \pi}, $$ then the cumulative distribution $F(\beta)= P(\theta_1<\beta | \theta_1 <\min(\theta_2,\theta_3)$ is $$ F(\beta)= \frac{\int_{\theta_1=0}^\beta \frac{2 \pi - 3 \theta_1}{2 \pi}\;d\theta_1}{\int_{\theta_1=0}^{2 \pi/3}\frac{2 \pi - 3 \theta_1}{2 \pi}\;d\theta_1} $$ $$ = \frac{\int_{\theta_1=0}^\beta \frac{2 \pi - 3 \theta_1}{2 \pi}\;d\theta_1}{\pi/3}. $$ The probability density function for $\theta_1$ given $\theta_1 <\min(\theta_2,\theta_3)$ is $$ F'(\theta_1) = \frac{\frac{2 \pi - 3 \theta_1}{2 \pi}}{\pi/3} = \frac3\pi - \frac{ 9\theta_1}{2 \pi^2} $$ which matches your histogram.

Answer 2

First of all, we simplify the problem by noticing that the angles $d\theta_k$ are the absolute differences between pairs of the original angles $\theta_k$. If we set one of the original angles to be $0$, this is equivalent to cutting a stick of length $2\pi$ into three pieces, by making two cuts whose position on the stick is uniformly distributed, and looking at the distribution of the length of the shortest piece.

The total stick length doesn't matter, so this ties into various problems based around randomly breaking a stick into segments. This question might be a good place to start looking for approaches to the problem that help with intuition. In particular, this answer gives some intuition for the minimum value's distribution. I'd also add that the minimum value has a triangular distribution in the simpler case where you have several IID uniform variables, so these sorts of distributions are fairly common.

As a rough explanation, consider the size of the maximum angle. This will naturally tend to be larger, and larger values mean that there is less room left on the circle for the two smaller angles to be greatly different from each other. Thus, the smallest angle will be more likely to be small. Since there's nothing to counteract this at very small values, the distribution for the minimum angle is skewed in the way you observed.