0

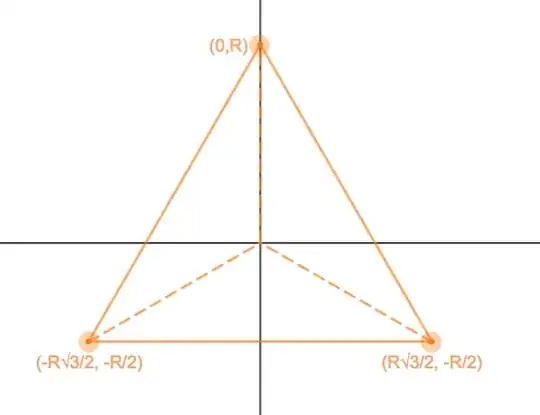
Is it possible to come up with a single-line equation in rectangular coordinates for an equilateral triangle with circumradius $R$, positioned symmetrical about the $y$-axis, as shown in the diagram below?

enter image description here

Hypergeometricx
  • 22,657
  • What do you mean by a “single-line equation?” This might be the sort of thing you’re looking for. – amd Jan 08 '19 at 19:36
  • @amd single-line equation meaning not a piecewise equation. Thanks for the suggested link - I did come across it earlier but here I'm looking for the solution for a specific case, and in rectangular coordinates. – Hypergeometricx Jan 09 '19 at 14:20
  • Can’t you adapt the accepted answer to that question to your specific case? – amd Jan 09 '19 at 19:34
  • Will take a look when I have some time. In the meantime, have posted my solution. – Hypergeometricx Jan 10 '19 at 17:38

3 Answers3

2

I’m not entirely satisfied with the following, but it works and generalizes to any cyclic polygon: $$\left(\sqrt3x+y-R\right)\left(\sqrt3x-y+R\right)\left(2y+R\right)+\sqrt{R^2-x^2-y^2}=\sqrt{R^2-x^2-y^2}.$$ The idea is that you take the union of the extensions of the triangle’s sides (the term on the left) and add terms that restrict the domain (the two radicals).

amd
  • 53,693
0

A possible solution is $$\big|y+x\sqrt3-R\big| \; +\;\big|y-x\sqrt3-R\big| \; +\;\big|2y+R\big|=3R+\delta$$ where $\delta$ is infinitesimal and $\delta>0$.

See desmos implementation here.

Each of the three terms on LHS within absolute value signs when equated to zero form the equations of the three sides of the triangle.

Interestingly, when $\delta=0$, the result is the entire region within the triangle.

Hypergeometricx
  • 22,657
  • You don’t find the “infinitesimal” fudge factor unsatisfactory? For any positive $\delta$, this is a hexagon, and when $\delta\lt0$, there is no real solution to this equation. – amd Jan 10 '19 at 18:58
  • I think it provides additional insight despite not being ideal. It's specified that $\delta$ is infinitesimal. The comment that $\delta>0$ has been added. – Hypergeometricx Jan 11 '19 at 14:19
  • That’s exactly what I myself find unsatisfactory: what exactly does “infinitesimal” mean? There is no real number $\delta$ for which this equation describes a triangle. The triangle is in some sense a limiting curve of these hexagons, but that’s a tricky thing to describe precisely. – amd Jan 11 '19 at 19:32
0

Here's a neat solution by my friend YC:

$$\frac 2{\sqrt3}\big| x \big| \; +\; \Bigg|\frac 43 y + \frac 2{\sqrt{3}}\ \big|x\big| - \frac R3 \Bigg| \; = \; R$$

See Desmos implementation here.

Hypergeometricx
  • 22,657