How to solve pell type equation

Question

Example $x^2-7y^2=2$ Find $x,y$ in general when $x,y$ are integer I don't know how to solve it , I need the method to help to solve it

Answer 1

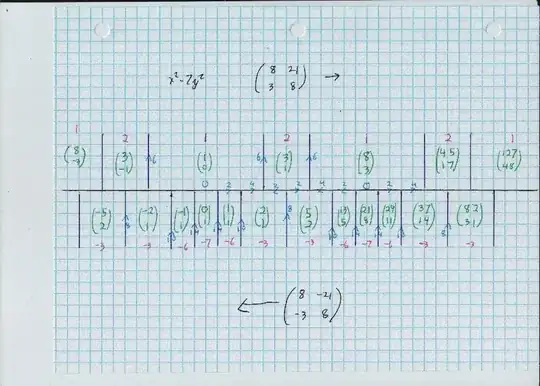
The diagram below shows everything you need. Below are four books that discuss Conway's topograph

Well, why not. It is unusual to get just a single one of these formulas: all solutions are given by arbitrary integer $n$ and $$ \left( \begin{array}{c} x_n \\ y_n \end{array} \right) = \left( \begin{array}{cc} 8 & 21 \\ 3 & 8 \end{array} \right)^n \left( \begin{array}{c} 3 \\ 1 \end{array} \right) $$

This leads to a single pair or Fibonacci type recurrences, $$ x_{n+2} = 16 x_{n+1} - x_n, $$ $$ y_{n+2} = 16 y_{n+1} - y_n. $$ These begin with $x_n$ as $$ 3, 45, 717, 11427, 182115,... $$ and $y_n$ in $$ 1, 17, 271, 4319, 68833,... $$

Most similar problems require more than one such fibonacci type "orbit." That is, more than one seed pair, call them $(x_0,y_0)$ and $(x_1,y_1),$ then follow with $ x_{n+2} = 16 x_{n+1} - x_n, y_{n+2} = 16 y_{n+1} - y_n. $

http://www.maths.ed.ac.uk/~aar/papers/conwaysens.pdf (Conway)

http://www.springer.com/us/book/9780387955872 (Stillwell)

https://www.math.cornell.edu/~hatcher/TN/TNbook.pdf (Hatcher)

http://bookstore.ams.org/mbk-105/ (Weissman)

If we switch to $x^2 - 7 y^2 = -3,$ we indeed get two orbits of type $$ x_{n+2} = 16 x_{n+1} - x_n, $$ $$ y_{n+2} = 16 y_{n+1} - y_n. $$

One orbit begins with $x_n$ and $y_n$ as $$ 2, 37, 590, 9403, 149858,... $$ $$ 1, 14, 223, 3554, 56641,... $$

The other orbit begins with $x_n$ and $y_n$ as $$ 5, 82, 1307, 20830, 331973,... $$ $$ 2, 31, 494, 7873, 125474,... $$

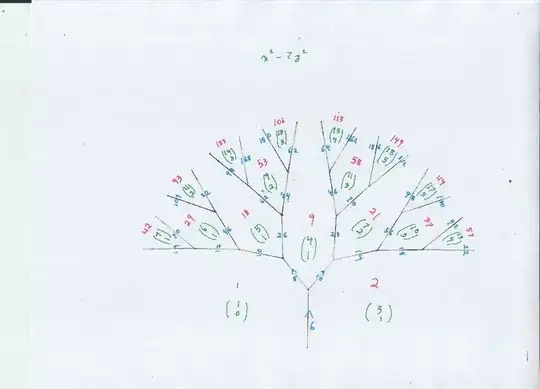
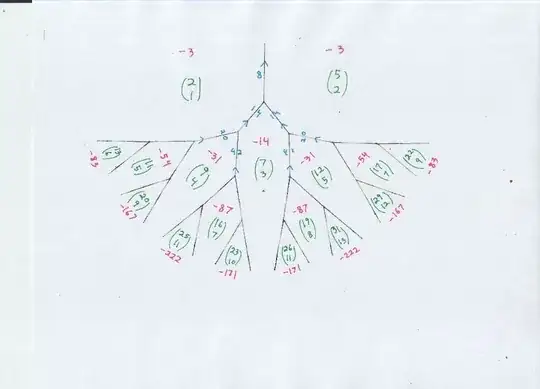
Just drew this, the tree below shows several of the small positive numbers that are primitively represented as $x^2 - 7 y^2,$ primitive meaning $\gcd(x,y) = 1.$ For most of these numbers, just one represention (green xy pair) is shown, so usually at least one more diagram will be needed to produce the recurrences.

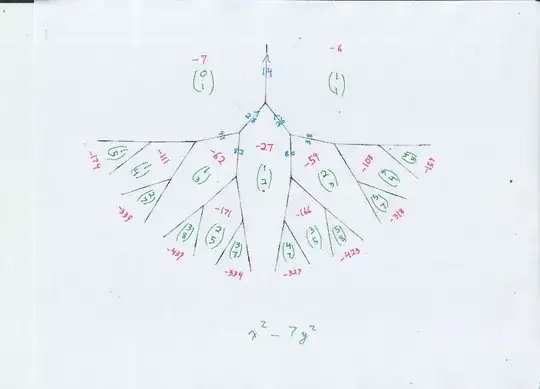
Here is one of the diagrams showing negative values of $x^2 - 7 y^2,$ therefore dropping downwards from the original "river" diagram. Also, while the light blue edge labels are important numbers, I am beginning to see why most authors do not draw them in the diagrams, they do clutter the picture. Also, when drawing one of my "tree" diagrams, it is obvious which way the blue arrows must point. I imagine I will draw in the first few blue edge labels..

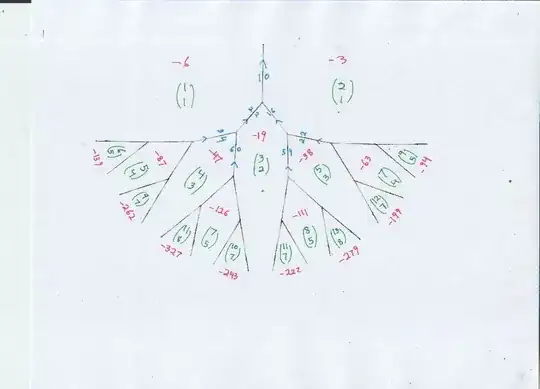Notice how, because of the symmetry $-3,-3$ at the "trunk" of the tree, all the values except the central $-14$ have two expressions within the diagram, thereby emphasizing that those values would need more than one orbit of recurrences (to parametrize all expressions as $x^2 - 7 y^2$)

Answer 2

Apply the PQa algorithm for D=7, determining that $\sqrt{7}=[2,\overline{1,1,1,4}]$

$ \begin{array}{c|c|c|c|c|c} j & P_j & Q_j & a_j & A_j & B_j \\ \hline 0 & 0 & 1 & 2 & 2 & 1\\ 1 & 2 & 3 & 1 & \textbf{3} & \textbf{1}\\ 2 & 1 & \textbf{2} & 1 & 5 & 2\\ 3 & 1 & 3 & 1 & \textbf{8} & \textbf{3}\\ 4 & 2 & \textbf{1} & 4 & 37 & 14\\ \end{array} $

From this (bold highlighted cells), we see that $3^2-7 \cdot 1^2 = 2$ and $8^2-7 \cdot 3^2=1$.

All solutions $(x_n,y_n)$ can then be found via $$x_n+y_n\sqrt{7} = (3+\sqrt{7}) \cdot (8+3\sqrt{7})^n$$ or via $$\begin{pmatrix}x_n&y_n\\7y_n&x_n\end{pmatrix} = \begin{pmatrix}3&1\\ 7&3\end{pmatrix} \begin{pmatrix}8&3\\ 21&8\end{pmatrix}^n$$ Or, equivalently (taking products of this type of matrices is commutative, and removing the redundancy) $$\begin{pmatrix}y_n\\x_n\end{pmatrix} = \begin{pmatrix}8&3\\ 21&8\end{pmatrix}^n\begin{pmatrix}1\\ 3\end{pmatrix} $$ Which is the same (but upside down) what Jagy mentions. Of course, this only works for $x^2-Dy^2 = k$ when $k < 2\sqrt{D}$. For general $k$, other methods are required (see Jagy's answer).