In how many ways can letters in a word CALCULUS be rearranged so that no two identical letters are adjacent?
I’ve been thinking of Inclusion-Exclusion principle. Is there any different way to solve this task?
In how many ways can letters in a word CALCULUS be rearranged so that no two identical letters are adjacent?
I’ve been thinking of Inclusion-Exclusion principle. Is there any different way to solve this task?
The answer is $2220$
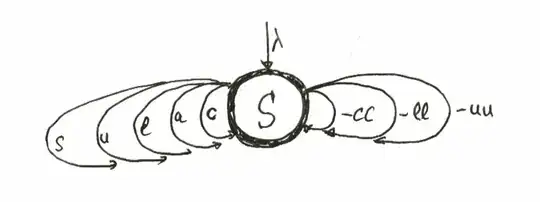 here is an automaton that generates CALCULUS-like words. To cover all possibilities, the S state must and suffice to be reached 5 to 8 times.
here is an automaton that generates CALCULUS-like words. To cover all possibilities, the S state must and suffice to be reached 5 to 8 times.
For each time, the generating function is
$$Z = (c+a+l+u+s - c^2 - l^2 - u^2)$$
where $+$ stands for inclusion, and $-$ for exclusion.
Now we take the coefficient of $c^2al^2u^2s$ in $Z^5+Z^6+Z^7+Z^8$ which is $2220$.
The explanation is that each occurence of a double letter in each word is generated twice, once with + and once with -. After summing, the terms containing double consecutive letters vanish.
There is no simpler method. If there were, the generating function would be simpler but that is not the case since I checked them all against the problems here.