3

I am having a very hard time with a problem from Gamelin's Complex Analysis.

Problem Statement and Hint: Show that if 0 and $\infty$ lie in different connected components of the complement $C^*\backslash D$ of $D$ in the extended complex plane, then there is a closed path $\gamma$ in $D$ such that $\int_{\gamma}d\theta\ne 0$. Hint. The hypothesis means that there are $\delta>0$ and a bounded subset $E$ of $C\backslash D$ such that $0\in E$, and every point of $E$ has distance at least $5\delta$ from every point of $C\backslash D$ not in $E$. Lay down a grid of squares in the plane with side length $\delta$ and let $F$ be the union of the closed squares in the grid that meet $E$ or that border on a square meeting $E$. Show that $\partial F$ is a finite union of a closed paths in $D$, and that $\int_{\partial f}d\theta=2\pi$

I've found a suggested proof online that says "Note by construction, $\partial F\subset D$. I've attached a picture which shows my grid of squares, set $D$ and set $E$ containing 0. I've outlined in green all of the squares that meet $E$ or that border on a square meeting $E$ (I think). The union of these closed squares in the grid is called F.

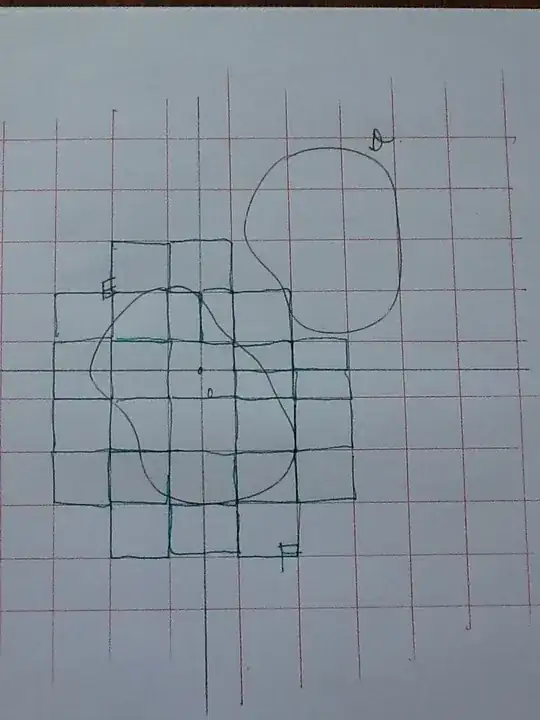
enter image description here

My first question is, how is $\partial F$, the border of $F$, contained in $D$?

David
  • 2,262

2 Answers2

2

One cannot simply choose $E$ as the component of $0$ in $D^c$, as this component may fail to be at positive distance from the rest of $D^c$. The existence of $E$ with required properties follows from the fact that (due to $D^c$ being compact in the topology of the sphere) the connected components of $D^c$ coincide with quasicomponents. That is, if two points $a,b\in D^c$ lie in different connected components of $D^c$, there are two disjoint clopen sets that contain $a$ and $b$ respectively. A proof of this topological fact can be found here. But my interpretation of

Hint. The hypothesis means that there are $\delta >0 $ and a bounded subset $E$ ...

is that Gamelin allows the reader to take the existence of $E$ for granted.

As for the question why $\partial F\subset D$, consider the following: if $z\in \partial F$, then at least one of the (closed) grid squares containing $z$ is not contained in $F$. Hence, this square is at a positive distance from $E$. Since this distance does not exceed $\delta\sqrt{2}$, the claim $z\in D$ follows from the properties of $E$.

Community
  • 1
ˈjuː.zɚ79365
  • 3,004
0

It's not clear how $E$ is choosen. I would choose $E$ to be the connected component of $C^*\setminus D$ which contains $0$. In that case the statement seems ok. The set $F$ contains $E$ and its boundary is far from other connected components of $C^*\setminus D$ hence $\partial F$ must be contained in $D$.

Emanuele Paolini
  • 21,447
  • OK, E is a connected component of $C^*\backslash D$ which contains 0. So it can't intersect the connected component that contains $\infty$. I see F contains E, but the statement $\partial F$ is far from the other components and must be contained in $D$ is what I don't see. Why is this so? And is it possible to draw an image to illustrate this point? – David Feb 17 '13 at 19:20
  • I assume $D$ is a connected open set. In general, it's not possible to choose $E$ to be the connected component of ${\Bbb C}^\setminus D$ that contains $0$, for example, if ${\Bbb C}^\setminus D$ is a Cantor set. Since ${\Bbb C}^\setminus D$ is closed in the compact Riemann sphere, its components and quasicomponents are the same, so you can partition ${\Bbb C}^\setminus D$ into two clopen sets so that $ 0$ and $\infty$ are in different parts. Then, you can let $E$ be the part containing $0$. – David Moews Feb 17 '13 at 22:32
  • @David: You choose $\delta$ small with respect to the distance from $E$ to the other connected components. Here you must assume that such distance is positive... this will require some regularity assumption on $D$. I think that if $D$ is the closure of its internal points you could prove that the distance is positive. – Emanuele Paolini Feb 17 '13 at 22:41
  • Probably, the assumption on $D$ is just that it's a connected open set, in which case the distance you mention need not be positive. – David Moews Feb 17 '13 at 22:45
  • @DavidMoews: in that case the proof suggested in the book would be completely inappropriate... and also the statement would be false. – Emanuele Paolini Feb 17 '13 at 22:54