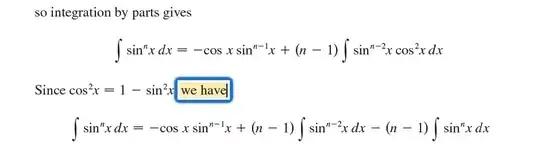distribution of constants over integrals

Question

I'm seeing this as part of a proof for the reduction formula and I see this:

So am I correct for saying that if you multiply the $sin^{n-2}{x}$ by $(1 - sin^2{x})$, you get $sin^{n-2}{x} - sin^n{x}$ and so the $(n-1) \int sin^{n-2}{x}\cdot cos^2{x}$ becomes what is shown below? is that right? Generally, $\int a - b = \int a - \int b$ right? That integral rule is visually intuitive right?

score 2 · Answer 1 · answered Jan 05 '19 at 01:51

2

Assuming that all of your functions are "nice", the integral operator is linear, and will split over sums and respects multiplication by constants. Formally, we have that $$ \int(af(x)+bg(x))\,dx = a\int f(x)\,dx + b\int g(x)\,dx $$ for all real numbers $a$ and $b$ and all functions $f$ and $g$ which have anti-derivatives.

answered Jan 05 '19 at 01:51

ItsJustTranscendenceBro

171

How does one define 'nice'? – Jan 05 '19 at 01:57
@DavidG I mentioned it in the final sentence; you need to be able to find anti-derivatives for both $f$ and $g$. The issue is that the class of functions which have anti-derivatives is difficult to characterize, so most of the time we pick a criterion that is way too powerful, like $f$ and $g$ are continuous. That would be enough to know that they have anti-derivatives, but it is not a necessary property. – ItsJustTranscendenceBro Jan 05 '19 at 01:59
Cheers, appreciate the detail. – Jan 05 '19 at 02:03
1

@DavidG For more information for anyone who reads this in the future (and you as well if you don't already know), you can look at this post for more info. – ItsJustTranscendenceBro Jan 05 '19 at 02:04
Awesome, I will check out. Thanks again. – Jan 05 '19 at 02:10

score 1 · Answer 2 · answered Jan 05 '19 at 01:50

Yes, the fact that $\int [a(x)-b(x)]dx$ is equal to $\int a(x)dx-\int b(x)dx$ is a well-known valid rule for manipulating integrals. This is also known as the "difference rule" for integrals. There is a good proof explaining why this rule is true on Paul's Online Notes.

In particular, your manipulation of these integrals above seems correct.

distribution of constants over integrals

2 Answers2