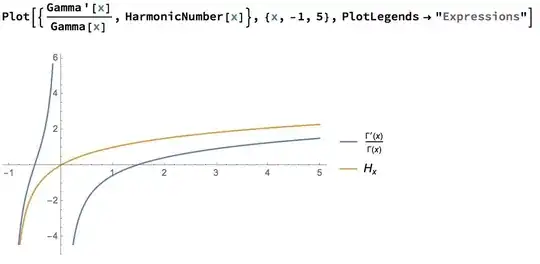
Let's try it in an elementary manner
- We can use the defining recursion of the harmonic number valid for $n\in Z^{+}$
$$H_{n} = H_{n-1} + \frac{1}{n}, H_{1}=1\tag{1a}$$
also for any complex $z$
$$H_{z} = H_{z-1} + \frac{1}{z}, H_{1}=1\tag{1b}$$
For instance for $z=1$ we obtain $$H_{1} = H_{0} + \frac{1}{1}$$
from which we conclude that $H_{0}=0$.
If we try to find $H_{-1}$ we encounter the problem that from $H_0 = 0 = \lim_{z\to0}(H_{-1+z} + \frac{1}{z})$ we find that $H_{z} \simeq \frac{1}{z}$ for $z\simeq 0$. In other words, $H_{z}$ has a simple pole at $z=-1$.
Hence we cannot continue in this manner to go to further into the region of negative $z$, so let us move to the following general approach.
- Starting with this formula for the harmonic number which is valid for $n\in Z^{+}$
$$H_{n} = 1+\frac{1}{2}+ ... + \frac{1}{n}\\\\=\frac{1}{1}+ \frac{1}{2}+ ... + \frac{1}{n} +\frac{1}{1+n}+\frac{1}{n+2} + ... \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;-\frac{1}{1+n}- \frac{1}{n+2} + ...\\=\sum_{k=0}^\infty \left(\frac{1}{k}-\frac{1}{ (k+n)}\right)\tag{2}$$
The sum can be written as
$$H_{n}= \sum_{k=1}^\infty \frac{n}{k (k+n)}\tag{3}$$
and this can be extended immediately to complex values $z$ in place of $n$
$$H_{z}= \sum_{k=1}^\infty \frac{z}{k (k+z)}=\sum_{k=1}^\infty \left(\frac{1}{k} -\frac{1}{k+z}\right)\tag{4}$$
This sum is convergent (the proof is left to the reader) for any $z$ except for $z=-1, -2, ...$ where $H_{z}$ has simple poles with residue $-1$.
Hence $(4)$ gives the analytic continuation.
For instance close to $z=0$ we have as in 1. that
$$H_{z} \simeq z \sum_{k=1}^\infty \frac{1}{k^2} = z\;\zeta(2) =z\;\frac{\pi^2}{6}\to 0 $$
We can also derive an integral representation from the second form of $(4)$ writing
$$\frac{1}{k} -\frac{1}{k+z} =\int_0^1 (x^{k-1}-x^{z+k-1})\,dx $$
Performing the sum under the integral is just doing a geometric sum and gives
$$H_{z} = \int_0^1 \frac{1-x^{z}}{1-x}\,dx \tag{5}$$
- $H_{z}$ at negativ half integers ($z = -\frac{1}{2}, -\frac{3}{2}, ...$)
These can be calculated from $(1b)$ as soon as $H_{\frac{1}{2}}$ is known.
So let us calculate $H_\frac{1}{2}$.
Consider
$$H_{2n} = \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{2n}$$
Splitting even and odd terms gives
$$H_{2n}=
\frac{1}{1} + \frac{1}{3} + \frac{1}{5} + ... + \frac{1}{2n-1}\\+
\frac{1}{2} + \frac{1}{4} + ... + \frac{1}{2n}\\=
\sum_{k=1}^n \frac{1}{2k-1} + \frac{1}{2} H_{n}\tag{6}$$
Now for the sum of the odd terms we write as in $(1)$
$$O_{n} = \sum_{k=1}^\infty \left(\frac{1}{2k-1} - \frac{1}{2(n+k)-1}\right)\tag{7}$$
This can be anlytically continued to any complex $n\to z$.
Replacing as before the summand by an integral and doing the summation under the integral gives
$$O_{z} = \int_0^1 \frac{1-x^{2z}}{1-x^2}\,dx\tag{8} $$
Substituting $x \to \sqrt{t}$ we find
$$O_{z} = \frac{1}{2}\int_0^1 \frac{1}{\sqrt{t}}\frac{1-t^{z}}{1-t}\,dt\\=
\frac{1}{2}\int_0^1 \frac{1-t^{z-\frac{1}{2}}}{1-t}\,dt-
\frac{1}{2}\int_0^1 \frac{1-t^{-\frac{1}{2}}}{1-t}\,dt\\
=\frac{1}{2}H_{z-\frac{1}{2}}+\log{2}\tag{9}$$
Hence $(6)$ can be written as
$$H_{2z} = \frac{1}{2} H_{z} +\frac{1}{2} H_{z-\frac{1}{2}}+\log{2}\tag{10} $$
Letting $z=1$ this gives
$$H_{2} = \frac{1}{2} H_{1} +\frac{1}{2} H_{\frac{1}{2}}+\log{2} $$
from which we deduce finally
$$H_{\frac{1}{2}} = 2(1-\log{2})\simeq 0.613706 \tag{11}$$
EDIT
Altenatively, the calculation of $H_{\frac{1}{2}}$ can be done using $(5)$ with the substitution $(x\to t^2)$:
$$H_{\frac{1}{2}} = \int_0^1 \frac{1-x^{\frac{1}{2}}}{1-x}\,dx
= 2\int_0^1 t \frac{(1-t)}{{1-t^2}}\,dt = 2\int_0^1 t \frac{(1-t)}{(1+t)(1-t)}\,dt \\=2\int_0^1 \frac{t}{{1+t}}\,dt=2\int_0^1 \frac{1+t}{{1+t}}\,dt -2\int_0^1 \frac{1}{{1+t}}\,dt = 2 - 2 \log(2)$$
and we have recovered $(11)$.
As an exercise calculate $H_{\frac{1}{n}}$ for $n =3, 4,...$.
I found that Mathematica returns explicit expression up to $n=12$ except for the case $n=5$. I have not yet understood the reason for this exception. Maybe someone else can explain it?
EDIT 2
Mathematica does readily calculate explicit expression using the formula
$$H_{\frac{1}{n}}=\sum_{m=1}^{\infty} \left(\frac{1}{m} - \frac{1}{m+\frac{1}{n}}\right)$$
For the previouly missing case $n=5$ we find
$$H_{\frac{1}{5}} = \frac{1}{4}\left(20-2\pi \sqrt{1+\frac{2}{\sqrt{5}}}-2 \sqrt{5}\; \; \text{arccoth}(\sqrt{5})-5 \log(5) \right)$$
For $n=7$ the result is a typical combination of trigonometric and log functions
$$H_{\frac{1}{7}} = 7 - \frac{\pi}{2} \cot ( \frac{\pi }{7}) - \log(14) -
2 \cos(\frac{\pi}{7}) \log(\cos(\frac{\pi}{14})) -
2 \sin(\frac{\pi}{14}) \log(\cos(\frac{3 \pi}{14})) \\+
2 \sin(\frac{3 \pi}{14})\log(\sin(\frac{\pi}{7})) $$
The general case for $n=1,2,3,...$ can be done by starting from the integral representation $(5)$ with $z=\frac{1}{n}$ using the substitution $x\to t^n, dx \to n t^{n-1} dt$ so that
$$H_{\frac{1}{n}}=n \int_{0}^{1} t^{n-1}\frac{1-t}{1-t^n}\;dt$$
Partial fraction decomposition leads to a simplification where the integrals can be solved elementarily. I shall leave the details to another occasion.