5

My aim is to find the number of rectangles (squares included) in a $n \times n$ grid. It is easy to get that result with combinations. The usual answer to this problem is given by

$$\binom{n+1}{2}^2$$

which makes sense, just select two parallel lines from the $n+1$ vertical lines and another two from horizontal ones. Intriguingly, this is the same as the sum of the first $n$ cubes: that is

$$1^3 + 2^3 + 3^3 + ... +n^3 = \binom{n+1}{2}^2$$

Are these two problems (the number of rectangles and the sum of cubes) and their results interrelated? Is there some sort of geometric connection between the two, and, if so, what is it?

PrincessEev
  • 43,815
Chirag Mehta
  • 109

2 Answers2

2

So it would take some effort to create the figure, but here is the math.

Let $N_k=\{i| 1\leq i \leq k\}$.

Consider an $(n+1)$x$(n+1)$ grid of points $\{(i,j)| \{i,j\}\subset N_{n+1}\}$ . The number of rectangles with vertices on those points is $\sum_{i=1}^n i^3$. If we consider the upper left subgrid of $n$x$n$ points, there are $\sum_{i=1}^{n-1} i^3$ rectangles within the upper left $n$x$n$ subgrid.

Subtracting, we find that there are exactly $n^3$ rectangles with a vertex on either 1) the right side of the $(n+1)$x$(n+1)$ grid or 2) the bottom of the $(n+1)$x$(n+1)$ grid. Call this set of rectangles $S$. We will group these $n^3$ rectangles into two disjoint sets: set $R$ - the rectangles with a vertex on the right side of the $(n+1)$x$(n+1)$ grid, and set $B$ - the rectangles with a vertex on the bottom of the $(n+1)$x$(n+1)$ grid that do not have a vertex on the right side of the grid.
$$S=R\cup B.$$

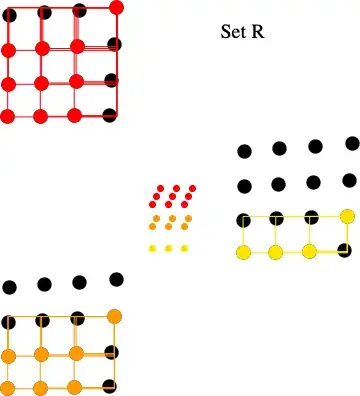
SET R

We can further divide set $R$ into $n$ disjoint subsets:

  • subset $R_1$ the rectangles whose upper right vertex is $(n+1,n+1)$,
  • subset $R_2$ the rectangles whose upper right vertex is $(n+1,n)$,
  • ...
  • subset $R_{n-1}$ the rectangles whose upper right vertex is $(n+1,3)$, and
  • subset $R_n$ the rectangles whose upper right vertex is $(n+1,2)$.

The cardinality of $R_i$ is $n\cdot(n-i+1)$ where $1\leq i\leq n$.

Consider the sets $$C= \{(i,j,k) | \{i,j,k\}\subset N_n\},$$ $$C_R= \{(i,j,k) | \{i,j,k\}\subset N_n, i\leq j\},\mathrm{\ and}$$ $$C_B= \{(i,j,k) | \{i,j,k\}\subset N_n, i> j\}.$$

Note that $C$ is the disjoint union of $C_R$ and $C_B$.

Also notice that the intersection of $C_R$ and the set of points with x-coordinate is 1 has exactly $n^2$ points which happens to be the cardinality of $R_1$. The intersection of $C_R$ and the set of points with x-coordinate is 2 has exactly $n\cdot(n-1)$ points which happens to be the cardinality of $R_2$. Continuing in this fashion, we can see that there is a 1-1 correspondence between the rectangles in $R$ and the points in $C_R$. $$|R|=|C_R|.$$

enter image description here

SET B

We can divide set $B$ into $n-1$ disjoint subsets:

  • subset $B_1$ the rectangles whose lower right vertex is $(n,1)$,
  • subset $B_2$ the rectangles whose upper right vertex is $(n-1,1)$,
  • ...
  • subset $B_{n-2}$ the rectangles whose upper right vertex is $(3,1)$, and
  • subset $B_{n-1}$ the rectangles whose upper right vertex is $(2,1)$.

The cardinality of $B_i$ is $n\cdot(n-i)$ where $1\leq i\leq n-1$.

Notice that the intersection of $C_B$ and the set of points with x-coordinate is $n$ has exactly $n\cdot (n-1)$ points which happens to be the cardinality of $B_1$. The intersection of $C_B$ and the set of points with x-coordinate is $(n-1)$ has exactly $n\cdot(n-2)$ points which happens to be the cardinality of $B_2$. Continuing in this fashion, we can see that there is a 1-1 correspondence between the rectangles in $B$ and the points in $C_B$. $$|B|=|C_B|.$$

We have shown that there is a 1-1 correspondence between the set of rectangles with a vertex either on the right side or the bottom of the $(n+1)$x$(n+1)$ grid of points and the points in an $n$x$n$x$n$ cube of points.

Induction could now be used to prove that the number of rectangles with vertices on a $(n+1)$x$(n+1)$ grid of points is $\sum_{i=1}^{n} i^3$.

Drawing all of this is possible but cumbersome.

irchans
  • 1,915
  • 2
    I think that in about an hour I could create a visually compelling diagram that shows that $f(n+1)-f(n) = n^3$ where $f(n)$ is the number of rectangles which can be formed by placing their vertices at points located in an $n$x$n$ grid of points. Right now it does not seem to be worth the time because I imagine that no more than 10 people would ever see it. – irchans Jan 03 '19 at 15:30
1

Let $R(k)$ be the number of rectangles whose width and height are both larger than $k$. These are specified by two ordered pairs $(r_1,r_2)$ and $(c_1,c_2)$ where $r_2\ge r_1+k$ and $c_2\ge c_1+k$. Consider the ordered pairs $(r_1,r_2-k+1)$ and $(c_1,c_2-k+1)$. In both of these, the second entry is larger than the first, and both entries are between $1$ and $n-k+1$. There are $\binom{n-k+1}2$ ways to choose the modified ordered pair $(r_1,r_2-k+1)$, so the number of such rectangles is $$\binom{n-k+1}2^2.$$ Now, let us count the number of rectangles whose smallest dimension is equal to $k$. I claim this is $R(k-1)-R(k)$; we take rectangles whose dimensions are both at least $k$, and subtract the rectangles whose dimensions are both more than $k$, leaving rectangles with at least one dimension equal to $k$ and the other at least $k$. The result is $$ R(k-1)-R(k)=(n-k+2)^2(n-k+1)^2/4-(n-k+1)^2(n-k)^2/4=\boxed{(n-k+1)^3.} $$ Summing over $k$, we see that the total number of rectangles is the sum of $(n-k+1)^3$, so is a sum of cubes.

Mike Earnest
  • 75,930