Let $C\subseteq\mathbb{R}^2$ be connected, open and have a bounded complement. Let $u\in C$ and $f:[0,1]\rightarrow \mathbb{R}^2$ be a continuous injective function such that $f(0)=u$. It is also given that $f([0,1))\subseteq C,f(1)\notin C$. Does it follow that $C-f([0,1])$ is connected ?
I really think that the answer is yes and the proof would be short, however I can't figure it out.
Since $C$ is open and connected, it is also path-connected. Let $C' = C \setminus \operatorname{img}(f)$. We prove that $C'$ too is path-connected.
Let $a, b ∈ C'$ and $γ \colon [0..1] → C$ be a path connecting those two points. If $\operatorname{img}(γ) ⊂ C'$ then there is nothing to show.
So let's assume $\operatorname{img}(γ) \not⊂ C'$, meaning $\operatorname{img}(γ) ∩ \operatorname{img}(f) ≠ ∅$. The intersection of those paths must be closed, so following $γ$ we eventually arrive at a first point of intersection (which isn't $a$) and at a last point of intersection (which isn't $b$).
Now since is $[0..1]$ is compact, $\operatorname{img}(f)$ is hausdorff, $f$-images of closed sets are indeed closed in the image of $f$ and since $f$ is injective, $\operatorname{img}(f)$ is indeed homeomorphic to $[0..1]$.
This implies that $\operatorname{img}(f)$ is locally connected, so we can cover it with a corresponding collection of open disks. We can find a Lebesgue number $r > 0$ such that any $r$-ball around a point in $\operatorname{img}(f)$ lies in the union of the covering.
Now their union yields some kind of inflation of the path $f$, so that it is open.
The idea is to jiggle $f$ around in this inflation such that it continues $γ$ to $a$ and $b$. But I fear I can't finish this argumentation, for one has to consider the boundary as well and I'm getting tired. So instead I made this beautiful picture in gimp using my trackpoint:
The complement of an open set $U$ in $\mathbb{R}^2$ consists of a union of simply connected sets iff $U$ is open. Notice that deleting the arc is the same as adding an arc to a closed set which is a component of the complement. But the closed set plus the arc clearly deformation retracts onto the original closed set, so it is simply connected iff the original is. So we see that adding the arc does not change the connectedness of the set.
The complement $\mathbb{R}^2 \backslash C$ is a homeomorphic image of finitely many disjoint closed balls. Now you can apply Jordan arc theorem, and you are done.
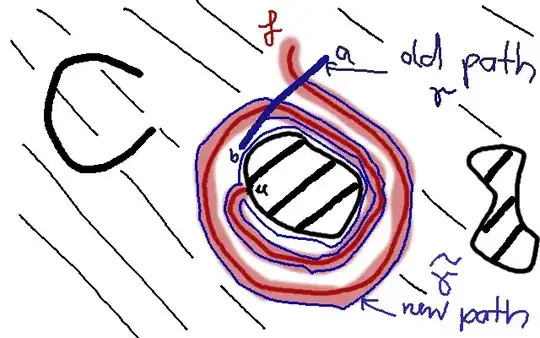
We can show that for every $x \in U \setminus f([0,1])$, we can get from $x$ to $u$ with a curve in $U \setminus f([0,1])$.
Let $g$ be the curve that connect between $x$ and $u$ in $U$. If $f$ and $g$ don't intersect, we're done.
Otherwise, let $y$ be the first point where the two curves intersect. $f$ is injective, therefore exists unique $0<t<1$ s.t. $ y=f(t)$.
The set $[0,t]$ is compact in $U$ open set, therefore there exists $\delta>0$ s.t. $B(f([0,t]), \delta) \subset U$. It's easy to see that the set $B(f([0,t]), \delta) \setminus f((0,t))$ is connected. So there exists a curve $h$ from $f(t)=y$ to $f(0)=u$ and by concatenation of $h$ with the first part of $g$ which connect from $x$ to $y$, we'll get a curve in $U \setminus f([0,1])$ from $x$ to $u$.
Edit: I've mistakenly shown that $U \setminus f((0,1))$ is connected. So to fix it, for $x,y \in U \setminus f([0,1])$, do the same process as describe above for $t_0,t_1$ where $f(t_0), f(t_1)$ are the first and last intersections of the original curve between $x$ and $y$ and the curve $f$.
