I read a solution in a book and here are the steps in it.
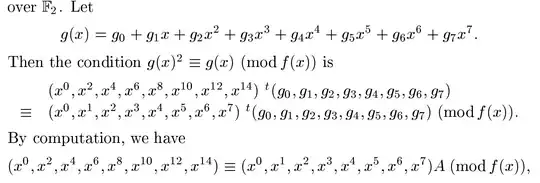

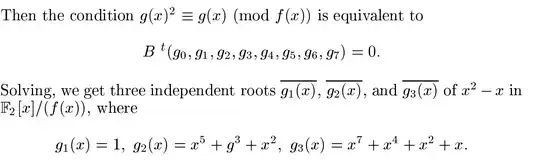
but I don't understand how $g_i(x)$ is got.So how did he get it or is there some other ways to find the answer?
I read a solution in a book and here are the steps in it.
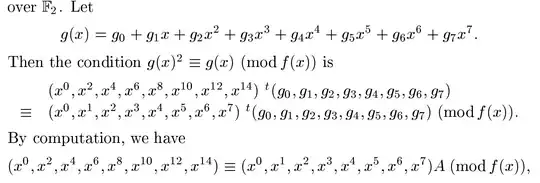

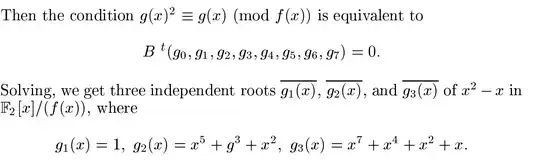
but I don't understand how $g_i(x)$ is got.So how did he get it or is there some other ways to find the answer?
Trial and error works well on this small example.
A polynomial over $\mathbb F_2$ is a multiple of $x+1$ iff it has an even number of nonzero terms. So for a start we can divide out factors of $x+1$ as long as we can: $$ \begin{align} & x^8 + x^4 + x^3+x^2+x+1 \\ ={}& (x+1)(x^7+x^6+x^5+x^4+x^2+1) \\ ={}& (x+1)^2(x^6+x^4+x+1) \\ ={}& (x+1)^3(x^5+x^4+1) \end{align} $$ Now if $x^5+x^4+1$ has further factors, they must be irreducible of degree $2$ and $3$, respectively, because we've already dealt with all possible factors of degree $1$ (namely $x+1$, and $x$ which is obviously not a factor).
So all that remains now is trying the irreducible polynomials of degree $2$ -- of which there is only one, namely $x^2+x+1$ (since $x^2+1$ is a multiple of $x+1$).
But by direct division we find that $$x^5+x^4+1=(x^2+x+1)(x^3+x+1)$$ so $$ x^8 + x^4 + x^3+x^2+x+1 = (x+1)^3(x^2+x+1)(x^3+x+1) $$
Describing what is going on as the other answerers seem to totally ignore the question body (for the reason that it is a bit lacking in explaining where the image came from).
A main idea in Berlekamp's algorithm, when trying to factor a polynomial $f(x)\in\Bbb{Z}_2[x]$, is to look for solutions $g(x)$ of the congruence $$ g(x)^2\equiv g(x)\pmod{f(x)}.\qquad(*) $$ Because we are in characteristic two this congruence is a homogeneous system of linear equations in the unknown coefficients of $g(x)=g_0+g_1x+g_2x^2+\cdots +g_7x^7$, in spite of appearances to the contrary! This follows from the characteristic two freshman's dream, $g(x)^2=\sum_j g_jx^{2j}$.
Assume that the factorization of $f(x)$ is $$ f(x)=\prod_{j=1}^kp_j(x)^{a_j}, $$ where $p_j(x)$ are distinct irreducible polynomials. By the Chinese remainder theorem $(*)$ is equivalent to a system of congruences $$ g(x)^2\equiv g(x)\pmod{p_j(x)^{a_j}},\quad j=1,2,\ldots,k. \qquad(**) $$ Now, any individual congruence in the system $(**)$ only has the trivial solutions $g(x)\equiv0$ and $g(x)\equiv1$ modulo the appropriate modulus. This is because only one of the factors of $g(x)^2-g(x)=g(x)(g(x)+1)$ can be divisible by $p_j(x)$, and hence has to be divisible by $p_j(x)^{a_j}$ for this congruence to hold.
Anyway, CRT says that any combination of solutions of the individual congruences can be lifted to a global solution of $(*)$. In particular, the solution space of $(*)$ has dimension $k$.
So the answer to OP's first question is that the polynomials $g_1,g_2,g_3$ were found by solving a linear homogeneous system of equations. The methods for doing that should be familiar to you from linear algebra. Basically a lot of row column operations and such. <- The author of the source writes the matrix of coefficients of a linear system to the right of the vector of the variables. This has the side effect that instead of the more common elementary row operations you should do elementary column operations to the matrix $B$ to find a basis for the solution space of $\vec{x} B=\vec{0}$.
How to proceed? Well, if a polynomial $g(x)\neq0,1$ is in the solution space, then we can find a non-trivial factor of $f(x)$! This is because, in view of the above, we must have $g(x)\equiv0$ modulo some factor $p_j(x)^{a_j}$ and $g(x)\equiv1$ modulo some other factor. This means that $\gcd(g(x),f(x))$ is a non-trivial factor of $f(x)$. I don't remember whether Berlekamp had even more efficient ideas at this point, but we can, at the very least, use the Euclidean algorithm to calculate $\gcd(g(x),f(x))$ for all non-constant polynomials $g(x)$ in the solution space.
Let's see, $g_2(x)=x^2(x^3+x+1)$, so as $f(x)$ is not divisible by $x$, we can conclude that $\gcd(g_2(x),f(x))$ must be equal to $x^3+x+1$. Similarly with $g_3(x)=x^7+x^4+x^2+x$ a run of Euclid reveals that $$ \gcd(g_3(x),f(x))=x^3+x^2+x+1=(x+1)^3. $$ Last but not least $$ \gcd(g_2(x)+g_3(x),f(x))=x^2+x+1. $$ That's it, all the factors accounted for!
Currently my favorite algorithm for factoring polynomials over a finite field is Cantor-Zassenhaus. See this post by yours truly for an annotated run of C-Z for something similar. Berlekamp's method is older, and IIRC has the benefit of being deterministic even if a bit slower in the average.
Cantor-Zassenhaus requires the polynomial to be factored to be square-free. That is easy to arrangeas a preliminary step, because any factor $p_j$ with multiplicity $a_j>1$ is a common factor of $f(x)$ and the formal derivative $f'(x)$. In the present case $$ f'(x)=x^2+1=(x+1)^2, $$ and we easily see that this time actually $f'(x)\mid f(x)$, readily implying that $(x+1)^3$ must be a factor of $f(x)$.
$$x^8+x^4+x^3+x^2+x+1=x^3(x^5-x^2+x^2+x+1)+x^2+x+1=$$ $$=(x^2+x+1)(x^3(x^2(x-1)+1)+1)=$$ $$=(x^2+x+1)(x^6-x^5+x^3+1)=$$ $$=(x^2+x+1)(x^6+x^5+x^3+1)=$$ $$=(x^2+x+1)(x^2+1)(x^4-x^2+1+x^3)=$$ $$=(x^2+x+1)(x^2+1)(x+1)(x^2(x-1)+x^2-x+1)=$$ $$=(x^2+x+1)(x+1)^3(x^3-x+1)=(x^2+x+1)(x+1)^3(x^3+x+1).$$