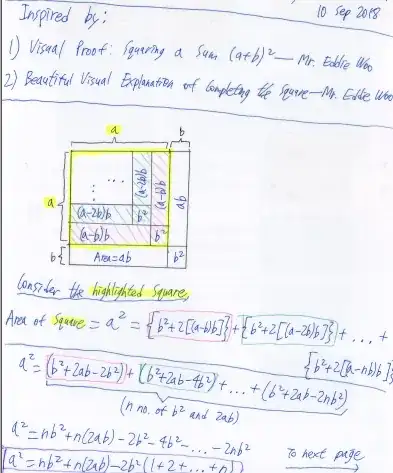
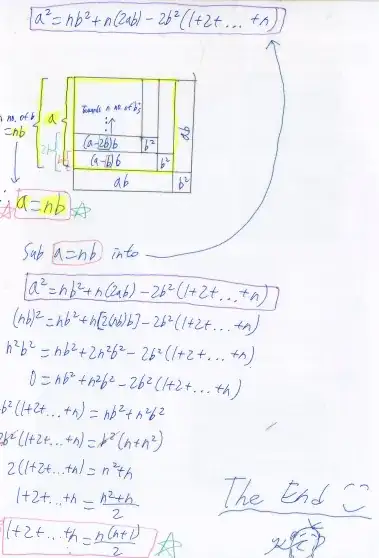
To be frank, I didn't learn any sort of proof for this (visual or non-visual), so I came up with this proof through trial and error.
Moreover, I haven't checked my proof online yet, therefore I am not sure if I am the first one to come up with this proof - Nonetheless, it is still quite a remarkable proof, at least for me :D.
Hope you will appreciate my visual proof from below!