We know $e^x = x$ has no real solution, and $1^x = x$ has a solution $x=1$.
For what value $1 < a < e$, $a^x = x$ has a real solution? (and no $b>a$ yields a solution.)
I do not have any context for the question, become curious when I used $x \leq e^x$. Appreciate any comment.
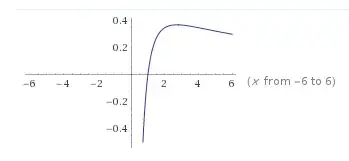
Taking logs of both sides of $e^{\log(a)x} = a^x = x$ gives $\log(a)x = \log(x)$, and rearranging gives $\frac{\log(x)}{x} = \log(a)$. The function $\frac{\log(x)}{x}$ takes values between $-\infty$ and $\frac{1}{e}$ (this is not too hard to check). Therefore, $a^x = x$ has a solution for any $0 < a < e^{\frac{1}{e}}$.
In fact, we can do better: $a^x = x$ has exactly one solution for $0 < a \leq 1$ and $a = e^{\frac{1}{e}}$, and exactly two solutions for $1 < a < e^{\frac{1}{e}}$. This can again be deduced by looking at the graph of $\frac{\log(x)}{x}$: 
This equation can be solved using a function known as Lambert $W$. It's the inverse of $f(x)=x e^x$
https://en.m.wikipedia.org/wiki/Lambert_W_function
Take your equation and write it as $e^{x \log (a)} =x$, then $-x\log( a) e^{-x \log (a)}= -\log( a)$, apply $W$ to get $-x \log( a)= W(-\log (a))$, so $x = -W(-\log (a))/\log (a)$.
