3

My problem is similar to this: Intuitive explanation for formula of maximum length of a pipe moving around a corner?

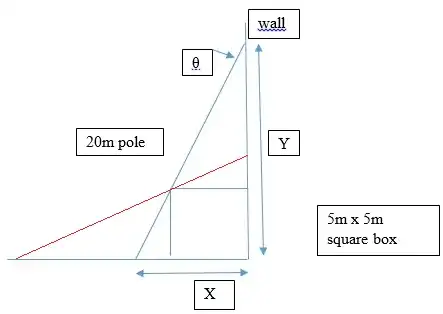
However my pipe (20m long) must pass through a specific point (5,5) in the X-Y plane and the question is then how high up the wall can it reach? - see diagram below. Diagram to explain setup

So my equations are $x^2 + y^2 = 400$ (function F) and the constraint can be written as $(x-5)(y-5) = 25$ (function G). This second equation is seen via above diagram as $tan(\theta) = x/y$ and also $tan(\theta)= 5/(y-5)$ and $tan(\theta)= (x-5)/5$ by similar triangles.

I use $ L = F - \lambda(G) $.

$ L = x^2 + y^2 - 20^2 - \lambda((x-5)(y-5)-25) $

So $\partial L_x = 2x - \lambda(y-5) = 0 $ Eqn1.

and $\partial L_y = 2y - \lambda(x-5) = 0 $ Eqn2

I then multiply Eqn1 by y and Eqn2 by x and subtract Eqn2 from Eqn1 and I cannot proceed from there. Below is a graph I did that shows the solution (6.811,18.805) for x and y, but I would like to be able to solve it via Lagrange multiplier. Thanks in advance for any clues Graph of the 2 Equations

dra42841
  • 31
  • 1
    we are trying to maximize $y$ subject to two constraints, $x^2+y^2=400$ and $(x-5)(y-5)=25$. Just solve the two equations – Lozenges Dec 22 '18 at 09:29
  • If you're going to use the similar triangles, then you could simply solve the system of equations $$ x^2 + y^2 = 400\ (x-5)(y-5) = 25 $$ and find those two intersections with positive coordinates. – Ben Grossmann Dec 22 '18 at 09:32
  • I'm not sure that this problem can be solved using Lagrange multipliers. What exactly is the quantity that you would be trying to maximize or minimize? – Ben Grossmann Dec 22 '18 at 09:37

1 Answers1

1

It is good that you want to make up a new problem and solve it. It is also good that you refer to the existing problem. Later on you can consider more difficult Moving sofa problem.

Now speaking of your problem, you need to clarify what you want to optimize. This is the question you pose:

the question is then how high up the wall can it reach?

It looks you want to maximize $y$ subject to two constraints: $$\begin{cases} x^2 + y^2 = 400 \ \ \ \ \ \ \ \ \ \ \ \text{(the pipe ends must touch the ground and the wall} \\ (x-5)(y-5) = 25 \ \ \text{(must pass through $(5,5)$)} \end{cases}$$

The thing is you can solve the two constraints as a system and find $(x,y)=(6.8; 18.8), (18.8; 6.8)$. And choose $y=18.8$ as a maximum.

See the only two choices (other lines will not satisfy both constraints):

$\hspace{3cm}$enter image description here

If you insist on solving the problem with Lagrange multiplier, then the Lagrange function is: $$L(x,y,\lambda_1,\lambda_2)=y+\lambda_1(400-x^2-y^2)+\lambda_2(25-(x-5)(y-5)).$$

Now you can set partial derivatives equal to zero and find $(x,y)$. Note that when you take partial derivatives w.r.t. $\lambda_1$ and $\lambda_2$, you will anyway get the system of two equations mentioned above, which produces the two solutions.

farruhota
  • 31,482
  • Thanks very much for that insight. I knew there were 2 solutions (via symmetry) but I never thought to put the extra y in the L (i.e. $L(x,y,\lambda_1,\lambda_2)=y+ $ ...etc ) - I also didnt think I would need two lambda's. Can you please explain how you can mathematically justify the extra y term in L, as all the examples I have seen just use the 2 functions as given and 1 lambda. I have also solved this problem using pure trigonometry (via a quadratic involving $Tan^2\theta$ and $Cot^2\theta$) but I was wanting to enhance my skills at the Lagrangian method. Thanks again – dra42841 Dec 22 '18 at 11:57
  • Hi again - On reflection I realize the answer to my query about the extra y is so obvious that I couldn't see it (must have been an off day) - y is the thing we are trying to maximize of course, so naturally it must be in the L. Thus the 2 Eqns I provided are BOTH constraints (and hence the need for $\lambda1$ and $\lambda2$ ) and I was trying to treat 1 of them as the thing I was trying to maximize-which was a wrong move on my part. – dra42841 Dec 23 '18 at 03:03
  • 1
    Yes, you explained it very well. As I said in the answer, you should always clarify what you want to optimize (here $y$, in the other problem, the length of pipe). In general, in the Lagrange function there will be as many lambdas as the number of constraints. Good luck. – farruhota Dec 23 '18 at 05:25
  • 1
    +1 for the good question and analysis. I see you are new to this forum. You can also upvote the answers you find useful, accept (hit the tick mark on the left) the answer that fully answers your questions or wait until better answers are provided. – farruhota Dec 23 '18 at 05:32