0

There is something I am misunderstanding about simplification. For example:

Given: $y^6$$z^6$/$x^6$

Why can I not take the 6th roof of both to simplify to $yz$/$x$? I clearly see that both expressions are not equal, yet I am tempted to make such a mistake. I realize that I cannot do this, perhaps someone can shed light on simplification rules. I realize this is a dumb question but I am revisiting math since I was never adept at it and I want to get good at it. My guess is that I am changing the value of it, and that simplifying is no longer taking place, I am not ordering everything into equal and less terms, I am changing the value. I get confused because it seems that I am just changing the proportions and not the value.

For context, I am reviewing exponent rules and here is a pic from the youtube video the problem is from: 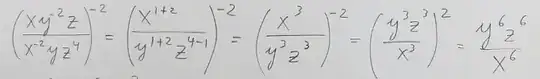enter image description here

I understand the exponent rules, I just was tempted to attempt to simplify more at the end.

Larry
  • 5,090
Sphygmomanometer
  • 231
  • 6
    You may write it as $\bigg(\frac{yz}{x}\bigg)^6$ – Mason Dec 22 '18 at 03:56
  • The mistake that you're making is known by educators as the "Law of Universal Linearity". An entire thread on this topic can be found here. :-) https://math.stackexchange.com/questions/630339/pedagogy-how-to-cure-students-of-the-law-of-universal-linearity – John Joy Dec 23 '18 at 14:22

2 Answers2

1

You can only divide both sides by the same factor. For example, if you had $\frac{6x}{6y}$, then you can divide both sides by $6$ and thus get $\frac{x}{y}$.

But there is no such common factor in $\frac {x^6}{y^6}$. The numerator has $6$ factors of $x$ ($x^6=x \cdot x \cdot x \cdot x \cdot x \cdot x$) and the denominator has $6$ factors of $y$ ($y \cdot y \cdot y \cdot y \cdot y \cdot y$)... meaning they have no common factors at all.

Compare:

$\require{cancel}$

$$\frac{6x}{6y}=\frac{6 \cdot x}{6 \cdot y}=\frac{\cancel{6}\cdot x}{\cancel{6} \cdot y}=\frac{x}{y}$$

$$\frac{x^6}{y^6}=\frac{x \cdot x\cdot x \cdot x \cdot x \cdot x}{y \cdot y \cdot y \cdot y \cdot y \cdot y} \text{ .... and there is nothing you can do}$$

Bram28
  • 100,612
  • 6
  • 70
  • 118
  • So given the $x^6/y^6$ ,Why couldn't I multiply the numerator and denominator by 1/6 and then be left with $x/y$? – Sphygmomanometer Dec 22 '18 at 03:58
  • @Sphygmomanometer you can, that is essentially what is done when you cancel the factor of 6.... as long as you multiply numerator and denominator by the same factor, you are OK – PhysicsMathsLove Dec 22 '18 at 04:00
  • @Sphygmomanometer You can .. but since neither side has a factor of $6$, nothing of interest would happen ... the one side only has a bunch of $x$'s, and the other side only has a bunch of $y$'s – Bram28 Dec 22 '18 at 04:00
  • @PhysicsMathsLove so if that is allowed, is the proper simplified form $x/y$? (following Bram28 example) – Sphygmomanometer Dec 22 '18 at 04:04
  • I understand what @Bram28 states, but it seems like I could stil get x/y by just taking the 6th root of numerator and denominator, which is wrong (every online simplification calculator states that $x^6/y^6$ is already simplified. – Sphygmomanometer Dec 22 '18 at 04:06
  • @Sphygmomanometer well the notion of the simplest form is not universal and tends to be with what you’re working with. Generally with high school maths, yes $ x/y$ would be the simplified form but also $xy^{-1}$ is perfectly acceptable. When dealing with quotients, just try to look for common factors and cancel these :) – PhysicsMathsLove Dec 22 '18 at 04:07
  • @Sphygmomanometer yes, because that is then a different quantity. When you square root it, you change the value of the expression, which is not what simplifying does. If you had p=x^6/y^6, then sure you can take the 6th root of both sides but now you are working with p^(1/6) and not p..... – PhysicsMathsLove Dec 22 '18 at 04:08
  • 2
    Ok I think I see my error, I am confusing simplifying with changing the value by performing operations on both numerator and denominator. So $x^6/y^6$ is already simplified to the fullest because there are no common factors that can be removed, by taking a root I am no longer in the business of simplifying, I am changing the value. Is this correct? – Sphygmomanometer Dec 22 '18 at 04:10
  • When you simplify, you want to reduce how much ‘stuff’ you have in the expression without changing the value. Cancelling the 6s make no difference and neither does cancelling any common factors because these would cancel when you put in any numbers. However if you took the 6th root, the value does change – PhysicsMathsLove Dec 22 '18 at 04:10
  • That sounds good to me... – PhysicsMathsLove Dec 22 '18 at 04:11
  • Just one more thing, when you say cancelling the 6s makes no difference, does it not make a difference though? x/y =! $x^6/y^6$ – Sphygmomanometer Dec 22 '18 at 04:12
0

Sometimes, but not very often, things can be cancelled that should not be cancelled. It's true that $\dfrac{19}{95}=\dfrac 15$, but, that the $9$s cancel is just a happy coincidence.

It's a common temptation to want to cancel things that shouldn't be cancelled. For example $\dfrac{x+6}{y+6} \ne \dfrac xy$.

You should be looking up what cancelling is and how it works. The most common form of cancelling works because $1\cdot x = x \cdot 1 = x$. For example

$$\dfrac{6x}{6y} = \dfrac 66 \cdot \frac xy = 1 \cdot \dfrac xy = \dfrac xy$$

In general, it just isn't true that $\dfrac{x^6}{y^6}= \dfrac xy \cdot \dfrac 66$. There are no laws of arithmetic that let you separate out the exponents like that.

Steven Alexis Gregory
  • 26,769