4

It is my first time that I met the word "entails". In mathematical texts, one usually sees "if and only if", "implies" or "iff" which bear no ambiguity. In the following definition:

enter image description here

Does "entails" mean "implies"? It certainly seems so. Also In one PHD thesis I am reading, the author quotes this definition using the word "implies" instead of the word "entails". So far so good, but next comes a corollary:

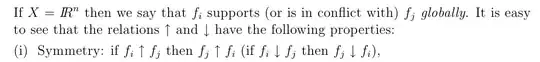
enter image description here

But if "entails" means "implies" then this corollary is not true. Since function

$$ f_1 \left( x \right) := x $$

clearly supports

$$ f_2 \left( x \right) := 1 $$

according to the definition above, but not the other way around.

This is because $x' \geq x \Rightarrow 1 \geq 1 $ but $ 1 \geq 1 $ does not imply $x' \geq x $ for all $x', x \in \mathbb{R}$.

What am I missing here?

Martin Drozdik
  • 812
  • 4
    It certainly means "implies", not "is equivalent to" (although to me - English not my first language - it sounds old and self-important, but maybe not). How or if this may have been used incorrectly here, I don't know (on cursory reading, I found those definitions/corollaries a bit confusing). – gnometorule Feb 15 '13 at 06:08
  • 3
    In English, when used in this context, the word "entails" generally means "implies" or "necessitates". It does not, generally speaking, mean "is equivalent to". In a more liberal interpretation, one can translate "entails" as "involves", which is somewhat closer to the notion of equivalence. Still, I'd agree with you that it appears to be misused here. – Elchanan Solomon Feb 15 '13 at 06:16
  • 2
    Thank you! So you think that the authors actually meant "iff"? I am really not sure, since both authors are British and the article is from 1995, so quite mature. – Martin Drozdik Feb 15 '13 at 06:19
  • 1
    I'm half-British and I don't recognize the word being used in this way. Regardless, I'd tentatively agree with you that it's best to assume they meant "iff". We can hopefully agree that Mathematicians, regardless of nationality, are more careful with the truth of their corollaries than with the finer details of semantics. – Elchanan Solomon Feb 15 '13 at 06:39
  • 1
    It might be worth reading this discussion http://math.stackexchange.com/questions/286077/implies-vs-entails-vs-provable It makes what I wrote look pretty amateurish. – bubba Feb 16 '13 at 10:53

2 Answers2

2

I'm 100% British (English, even), and I think this is strange and confusing usage.

According to my (American) thesaurus, some synonyms of "entails" are "brings about", "calls for", "demands", "causes", "gives rise to", "leads to", "necessitates", "requires".

From a logic/mathematics point of view, some of these terms mean "if" and some mean "only if".

I have never seen "entails" used to mean "equivalent to", and the thesaurus doesn't list this as a synonym, but who knows what these authors had in mind. Pretty poor writing, in my opinion.

Clarification of Synonyms

Let's split the terms into two groups:

I think it's clear that "brings about", "causes", "gives rise to", "leads to" all mean the same thing. Let's represent this group by "causes".

Similarly, I think "demands", "necessitates", "requires" all mean the same thing. Let's represent this group by "requires".

"A causes B" means that A implies B. In other words, "B is true if A is true".

"A requires B" means that "A can be true only if B is true"

So, in my view, the list of synonyms contains terms with two quite different meanings, which I (rather sloppily) characterised as "if" and "only if" terms.

bubba
  • 43,483
  • 3
  • 61
  • 122
  • 2
    Which of the synonyms you cited mean "if"? To me they all mean "only if", though with some variation of causality: if $X$ entails $Y$, then maybe $X$ causes $Y$, or maybe failure of $Y$ would prevent $X$ being possible (or it could be that $X$ just happens to never occur without $Y$, even in absence of causality; however I don't think any of the equivalents suggest that option). – Marc van Leeuwen Feb 15 '13 at 10:30
  • @Marc -- I added to my answer – bubba Feb 15 '13 at 14:38
2

You are perfectly right, and "entails" certainly should not be taken to mean "is equivalent to". I can just offer one possible explanation for this text: if $\geq$ is a total ordering and an "objective function" is always injective (so "ob" entails "in", I don't know the definition of "objective") then this relation is indeed symmetric. The function $f_2$ in your counterexample is of course not injective.

For in this case, assuming $f_i\uparrow f_j$ and $f_j(x')\geq f_j(x)$, one either has $x'=x$ and therefore $f_i(x')=f_i(x)$, or (by injectivity) $f_j(x')>f_j(x)$, whence (by $f_i\uparrow f_j$) it cannot be that $f_i(x')\leq f_i(x)$, so (by the total ordering) $f_i(x')>f_i(x)$; in summary we get $f_i(x')\geq f_i(x)$ in both cases.

I should add that "$X=\Bbb R^n$" in the citation makes it rather unlikely that objective functions are supposed to be injective. If this is about objective functions in optimization problems, which take their values in $\Bbb R$, then it is almost certainly wrong, as being injective is incompatible with being continuous for $n\geq2$. And for any non-injective objective functions you can do as you did in the counterexample.

Marc van Leeuwen
  • 115,048
  • This seems worth checking! – Tara B Feb 15 '13 at 10:38
  • Thank you! This certainly makes sense. But the authors do not mention injectivity. $f: \mathbb{R}^n \rightarrow \mathbb{R}$ is simply a generic function. – Martin Drozdik Feb 15 '13 at 10:41
  • What does 'objective function of (1)' mean? – Tara B Feb 15 '13 at 11:00
  • It is a generic function $f : \mathbb{R}^n \rightarrow \mathbb{R}$. It is explicitly mentioned that no other assumptions are made. – Martin Drozdik Feb 15 '13 at 11:08
  • That is, objective in the context of optimization. Objective functions are the functions whose supremum or infimum we are looking for. – Martin Drozdik Feb 15 '13 at 11:09
  • 1
    @MartinDrozdik: OK, so then my answer is not really applicable. It could be that you can save the corollary with some more realistic addition hypothesis on the $f_i$, for instance I think (for $X=\Bbb R^n$) it would be valid when the $f_i$ are piecewise differentiable and nowhere locally constant, or something like that. But even then it is certainly not worth being called a corollary. – Marc van Leeuwen Feb 15 '13 at 11:21
  • Thank you anyway! I always appreciate a second opinion. I also thought about saving the corollary with an additional assumption. – Martin Drozdik Feb 15 '13 at 11:30