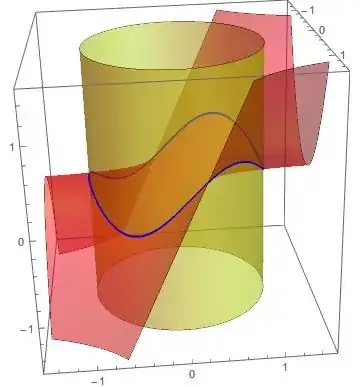
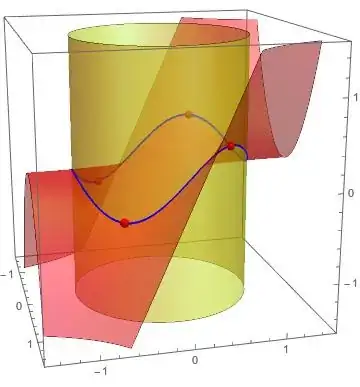
In a constrained optimization problem, let's consider the example $$\begin{cases}f(x,\ y) = yx^2\ \Tiny(function\ to\ be\ maximized) \\ g(x,\ y) = x^2 + y^2 = 1\ \Tiny(constraint)\end{cases}$$ why does the answer not need to satisfy $f(x^*,\ y^*) = 1$? Geometrically, viewing $f(x,\ y) = yx^2$ and $g(x,\ y) = x^2 + y^2$ in $ℝ^3$ (which motivated this question), why aren't solutions required to be points where $f(x,\ y)$ and $g(x,\ y)$ intersect, or at least where $f(x,\ y)$ intersects $g(x,\ y) = 1$? The solutions turn out to be $f(x^*,\ y^*, f(x^*,\ y^*)) = (±\frac{\sqrt6}{3},\ \frac{\sqrt3}{3},\ \frac{2\sqrt3}{9})$, which both have a height or $z$-coordinate of $\frac{2\sqrt3}{9}$, while I would expect any point that satisfies $g(x,\ y) = 1$ to have a height or $z$-coordinate of $1$. Instead of lying within the within the flat slice of the graph of $g(x,\ y) = x^2 + y^2$ where $g(x,\ y) = 1$, the solutions lie within the slice representing $g(x,\ y) = \frac{2\sqrt3}{9}$, seemingly failing to satisfy the constraint.
This worry can be obfuscated by flattening $ℝ^3$ into a contour plot where the constraint and maximized function do intersect, but only by discarding a dimension of information from the original picture; being aware of the 3D graph the contour plot represents, I still find the matter conceptually troublesome.
One proposed idea has been to view $g(x,\ y)$ as living in $ℝ^2$, thus ignoring its height/$z$-coordinate/output altogether. However, this seems unsatisfactorily at odds with its deep symmetry with $f(x,\ y)$, which lives in $ℝ^3$. Perhaps the labels and terminology in constrained optimization problems give the impression that the function and the constraint are dissimilar animals, but I get the feeling from my trivially faint glimpse of Lagrangian duality that they're actually highly symmetric. One is $f(x,\ y) = yx^2 =\ ????$, and the other $g(x,\ y) = x^2 + y^2 = 1$, and in fact, once solved, I can forget the $x*$ and $y*$ parts of the solution and reframe the problem where $f(x,\ y) = yx^2 =\ \frac{2\sqrt3}{9}$ is the constraint, and $g(x,\ y) = x^2 + y^2 =\ ????$ is the function, and I'll rediscover the same $x^*$ and $y^*$, along with the original constraint constant $1$. I have a hard time convincing myself that expressions with such symmetricity aren't properly viewed as equal in dimension.