3

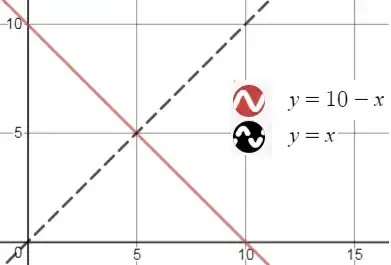
$f(x) = 10-x$

If I plugin $x=2$, I get $f(2)=10-2=8$.
If I want to know what I must plugin to get $8$, again I simply plugin $8$ into $f(x)$ : $f(8) = 10-8=2$.
One can conclude $f(x) = f^{-1}(x)$.

But this is not so clear to me. Specifically for this particular function $f(x)=10-x$, I'm trying to visualize using examples like, taking away $2$ apples from $10$ etc. But they don't seem to make much sense. I'm wondering if you have any other means to interpret $f(x)$.. Thanks in advance :)

AgentS
  • 12,195

4 Answers4

6

A function is self-inverse (that is $f(x)=f^{-1}(x)$) , if we have $$f(f(x))=x$$ This can be easily verified for this function.

Peter
  • 84,454
  • 1
    Another way to find this equation is to calculate $f^{-1}(x)$ for $f(x)=10-x$. We have $y=10-x$, which we can transform into $x=10-y$. Exchanging $x$ and $y$ leads to $y=10-x$, the original function. – Peter Dec 15 '18 at 10:14
  • 1
    Finally, you can verify the equation graphically by noting that the line $f(x)=10-x$ is symmetric with respect to the line $f(x)=x$, hence it is self-inverse. – Peter Dec 15 '18 at 10:18
  • 1
    Ahh right, any graph symmetric about $y=x$ is its own inverse because the points $(x,y)$ and $(y, x)$ exist on the same graph. Thank you so much :) – AgentS Dec 15 '18 at 10:20
  • Just for the record, a function that equals its own inverse is called an involution. – Andreas Rejbrand Dec 15 '18 at 13:59
6

The graph of the function $y=10-x$ is a straight line with the slope $-1$ and $y$-intercept $10$. If you reflect (see "Graph of the inverse" section) the straight line across $y=x$, you will get the line itself, because they are perpendicular. Hence the function is self-inverse. See the graph:

$\hspace{3cm}$enter image description here

farruhota
  • 31,482
3

$y=10-x \iff x=10-y$. This shows that $f(x) = f^{-1}(x)$.

Fred
  • 77,394
3

Using your analogy, this function partitions the apples into a "taken away group" and a "left over group".

If you take away 2, you have 8 left over.
If you have 8 left over, you took away 2.

This function is a map between # taken away <-> # left over.

pierrecurie
  • 149