Proving the interval $(0, 1)$ and $(1, 3)$ have the same cardinality.

Question

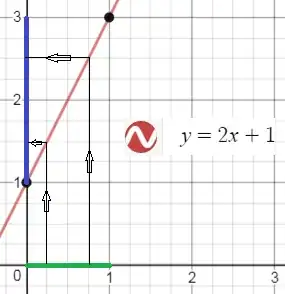
Prop: Show that the intervals $(0, 1)$ and $(1, 3)$ have the same cardinality.

What I have tried: I showed that the intervals $[2, 4]$ and $[0, 5]$ have equal cardinality by creating a function $F(x) = \frac52x - 5$. I did this by getting the length of both intervals, however, I don't understand why this works. In my notes, it shows that the length of $[2, 4]$ is $2$ but if we are including both endpoints shouldn't it be $3$? Same goes for the interval $[0, 5]$ we should have a length of $6$, not $5$, but when using $5/2$ and shifting everything by $-5$ it seems to work just fine.

Trying to solve this current prop: Because it is an open interval we cant use $0$ and $1$ from what I understand so I don't quite understand what to use as the length of this interval.

I have tried reading other questions similar to this one however I am still stumped.

Thanks for the support!

Answer 1

The length of an interval that starts at $a$ and ends at $b$ is $b-a$ regardless of whether the interval is open or closed at the endpoints (or half open). Adding one or both of $a$ and $b$ does not change the length. The simple linear transformation will not change the open or closed status of the endpoints. The length of $(0,1)$ is $1$ and of $(1,3)$ is $2$. The transformation from $(0,1)$ to $(1,3)$ given by $F(x)=2x+1$ works fine.

Answer 2

1) I don't believe I am confusing cardinality with the length I'm not sure if anyone understanding my question. Cardinality is the number of elements within a set and is used to check if a set is denumerable as an example. I don't understand what length is in this case if 0 or 1 is not included and that's what I'm trying to figure out, I have no idea how you got 2x with the open intervals of 1, 3 and 0, 1.

2) I understand that but I don't understand how we get the two length values from both intervals in order to create a function to show this one to one relationship.

You are right, the cardinality is "the number of elements within a set" (see here). For example, for the finite sets: $|\{1,2,3\}|=|\{5,6,7\}|=3$, because there are three elements in each set. Also, you can say the two sets have equal cardinality because there is a bijection from the first set to the second. Both of these sets are countable, because their cardinalities are finite. The term "denumerable" usually refers to "countably infinite" or $\aleph_0$ (the cardinality of the natural numbers), which does not apply here. The set of rational numbers is also denumerable (see here). See also this post for distinguishing the concepts.

The idea is the same for infinite sets. Note that $(0,1)$ and $(1,3)$ are uncountable, hence not denumerable. Yet, we can establish the equality of their cardinalities if we can find a bijection from one set to another. And we can, it is $f(x)=2x+1$, because every element of the first set can be injectively and surjectively matched with the elements of the second set. See the graph:

$\hspace{5cm}$

How do we find the linear relation? Just find the line passing through the two points: $$\frac{y-1}{3-1}=\frac{x-0}{1-0} \Rightarrow y=2x+1.$$

Answer 3

It is a basic fact that $(0,1)$ has the same cardinality with any interval $(a,b)$, for any $-\infty<a<b<\infty$.

The reason is that we can build a bijection from $(0,1)$ to $(a,b)$. Why does the bijection matter? Because it is our definition: if there exists a mapping $\varphi:A\rightarrow B$, $\varphi$ is a bijection (i.e.,$\varphi$ is 1-1 and onto), then we say $A$ and $B$ have the same cardinality. Notation: $|A|=|B|$.

As long as we find such a bijection, then our proof is finished. We do find a bijection, that is $\varphi(x)=a+(b-a)x$.

Now we check $\varphi$ is a bijection. First, suppose $\varphi(x_1)=\varphi(x_2)$, then we have $$a+(b-a)x_1=a+(b-a)x_2$$ that is $$(b-a)x_1=(b-a)x_2$$ thus $$x_1=x_2$$ So $\varphi$ is one-to-one.

Second, to say $\varphi$ is onto, $\forall y\in(a,b), a<y<b$, there must exist $x\in(0,1),s.t. \varphi(x)=y$. That is, $$a+(b-a)x=y$$ Let $x=\frac{y-a}{b-a}$. You can verify that $x\in(0,1)$ and $\varphi(x)=y$. So $\varphi$ is onto.

Together, we prove that $\varphi$ is bijection. Then according to definition, our proof is finished.

Answer 4

Note that cardinally is different from length or measure (in a more general sense). Cardinally is a generalisation of number of elements in a set. So by setting a 1-1 correspondence between two sets $A$ and $B$, we can show that the cardinality of the two sets are the same. This does not necessarily imply the 'length' (or measure) of both sets are the same.

---

Edit:

In showing a function $F: A \to B$ is a 1-1 correspondence (or bijective), one shall verify $F$ satisfies the following two properties:

1. (Injectivity) $\quad x = y \iff F(x) = F(y) \; \forall x,y \in A$
2. (Surjectivity) $\quad \forall \,y \in B, \exists \, x \in A $ such that $F(x) = y$

Now if $A$ and $B$ are intervals of $\mathbb{R}$, then we can construct a linear function (you can verify by yourself that linear function indeed construct a 1-1 correspondence between the two intervals). To construct that linear function, one shall consider informally as if first translate interval $A$ for certain amount and then 'dilate' or 'shrink' the interval for a certain amount to get 'B'. That 'dilating' or 'shrinking' factor should be the ratio of lengths of the two intervals.

Answer 5

Define $f:(0,1) \to (1,3)$ as $f(x)=2x+1$ this is a bijective function (I will leave you the proof), hence they have the same cardinality. I think you are confusing cardinality with measure (length). You should check that out.

Answer 6

To show equal cardinality of sets, you basically have to show a bijection, or one - to - one relationship exists between them.

For finite sets, you can just "count the elements", but that's actually establishing a bijection of both sets to a finite subset of the natural numbers.

For infinite sets, you have to come up with a one to one function that maps one set to the other.

It should be quite obvious a linear relationship will suffice here. That's a relationship of the form "$y=mx+c$". The relative lengths are simply to help you decide the "scaling factor" to go from one to the other. That decides $m$, the gradient or slope of the line. The value of $c$ (the "$y$ intercept) should be thought of as an offset or" zero error" to line up the respective initial points of the intervals.

So in the case of $(0,1) \rightarrow (1,3)$, the respective lengths are $1$ and $2$ (with a ratio of $2$) while the offset is $1$. So the function is $f(x) = 2x +1$, and that's the bijection that proves equal cardinality.

The lengths of the interval are only important in finding that $m$ value. They don't directly impact cardinality.