How would we evaluate the below integral by methods of complex analysis?
$$\int_{0}^{1} \frac{\ln(x+1)}{x^2+1} \mathrm{dx}$$
I asked the question a while ago, but at that time I didn't specify this requirement.
Now, I'm only interested in a complex way. Thanks !!!
Sis.
Well, there is a method which is not that complex.
$$\int_0^1 \frac{\log(1+x)}{1+x^2}dx$$
$$\int_0^1 \left(\int_0^x \frac{1}{1+y}dy\right)\frac{1}{1+x^2}dx$$
$$\int_0^1 \int_0^x \frac{1}{1+y}dy\frac{1}{1+x^2}dx$$
Make a change of variables $y=ux$ in the inner integral:
$$\tag 1 \int_0^1 \int_0^1 \frac{x}{1+ux}\frac{1}{1+x^2}dudx$$
Partial fractions:
$${x \over {1 + xu}}{1 \over {1 + {x^2}}} = {1 \over {1 + {u^2}}}{x \over {1 + {x^2}}} + {u \over {1 + {u^2}}}{1 \over {1 + {x^2}}} - {u \over {1 + {u^2}}}{1 \over {1 + xu}}$$
Now, integrating the first two terms, which account to the same$^1$, gives that you integral is
$$\mathcal I=\frac \pi 4\log 2-\int_0^1\int_0^1 \frac u {1+u^2}\frac{1}{1+xu}dxdu$$
The latter integral is just our original integral, due to symmetry, as you see in $(1)$
This means that $$\mathcal I =\frac \pi 8 \log 2$$
as desired. You can see a simlar integral solved here with the very same method.
$1$: symmetry, once again.
We have $$ \int_0^1 \frac{\ln(1+x)}{x^2+1}dx= \left[\begin{array}{l} t=\frac{1}{x} \\ dt=-\frac{1}{x^2}dx \end{array}\right]=\int_1^\infty \frac{\ln(t+1)-\ln{t}}{1+t^2}dt= \left[\begin{array}{l} u=t-1 \\ du=dt \end{array}\right] = \int_0^\infty \frac{\ln(u+2)-\ln(u+1)}{1+(u+1)^2}du. $$
I am quite confident that this integral can be handled with a keyhole contour in much a similar way as this integral. If you want me to do more details, just comment, and I will update when I have the time.
EDIT: Continued the argument. Please notify me about misprints or other errors. I will show how to compute $$\int_0^\infty \frac{\ln(x+2)}{1+(x+1)^2}dx$$ (the other one is solved analogously).
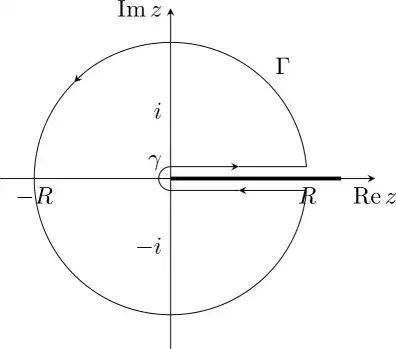
We now consider the integral $$\int_C \frac{\log^2(z+2)}{1+(z+1)^2}dz,$$ where $C$ is the keyhole contour above. Note the choice of logarithm! It is imperative that we take $0<\arg{z}<2\pi$ for the logarithms (or $2\pi n<\arg{z}<2\pi (n+1)$ for some $n\in\mathbb{Z}$).
The integrand has poles at $z=-1\pm i$, and by Cauchy's integral formula, we get $$ \int_C \frac{\log^2(z+2)}{1+(z+1)^2}dz= \int_C \frac{\log^2(z+2)}{(z+1+i)(z+1-i)}dz= 2\pi i\left(\frac{\log^2(1-i)}{-2i}+ \frac{\log^2(1+i)}{2i}\right)= \pi(\log^2(1+i)-\log^2(1-i))= \pi\left(\left(\ln\sqrt{2}+\frac{i\pi}{4}\right)^2-\left(\ln\sqrt{2}+\frac{7i\pi}{4}\right)^2\right)= \frac{6\pi^3-3i\pi^2\ln{2}}{2} .$$
The integral along $\gamma$ goes to zero as the inner radius goes to zero, and the integral along $\Gamma$ goes to zeros as $R\rightarrow\infty$ (this can be shown using the ML-inequality).
Therefore, in the limit we only get contributions from the straight parts, so $$ \int_0^R\frac{\log^2(x+i\varepsilon+1)}{(1+x+i\varepsilon)^2+1}dx+ \int_R^0\frac{\log^2(x-i\varepsilon+1)}{(1+x-i\varepsilon)^2+1}dx\rightarrow \frac{6\pi^3-3i\pi^2\ln{2}}{2}. $$ But we also have $$ \int_0^R\frac{\log^2(x+i\varepsilon+2)}{(1+x+i\varepsilon)^2+1}dx+ \int_R^0\frac{\log^2(x-i\varepsilon+2)}{(1+x-i\varepsilon)^2+1}dx\rightarrow \int_0^\infty\frac{\ln^2(x+2)-\left(\ln(x+2)+2i\pi\right)^2}{(1+x)^2+1}dx= \int_0^\infty\frac{4\pi^2-4i\pi\ln(x+2)}{(1+x)^2+1}dx, $$ so $$\int_0^\infty\frac{4\pi^2-4i\pi\ln(x+2)}{(1+x)^2+1}dx=\frac{6\pi^3-3i\pi^2\ln{2}}{2}.$$ By considering the imaginary part, we get that $$\int_0^\infty \frac{\ln(x+2)}{(x+1)^2+1}dx=\frac{3\pi\ln{2}}{8}.$$
It is possible to compute $$\int_0^\infty \frac{\ln(x+1)}{(x+1)^2+1}dx$$ analogously, and then take the difference in order to find the value of the original integral.
Here is a real method, and since $\mathbb{R}\subset\mathbb{C}\dots$ $$ \begin{align} \int_0^1\frac{\log(1+x)}{1+x^2}\mathrm{d}x &=\int_0^{\pi/4}\log(1+\tan(u))\,\mathrm{d}u\\ &=\int_0^{\pi/4}\Big(\log(\cos(u)+\sin(u))-\log(\cos(u))\Big)\,\mathrm{d}u\\ &=\int_0^{\pi/4}\Big(\log(\sqrt2\cos(\pi/4-u))-\log(\cos(u))\Big)\,\mathrm{d}u\\ &=\int_0^{\pi/4}\Big(\log(\sqrt2)+\log(\cos(\pi/4-u))-\log(\cos(u))\Big)\,\mathrm{d}u\\ &=\frac\pi8\log(2)\tag{1} \end{align} $$
Another method, avoiding all trig substitutions, and using contour integration
Suppose that $$ (1+x)(1+y)=2\tag{2} $$ That is, $$ x=\frac{1-y}{1+y}\quad\text{and}\quad\frac{\mathrm{d}x}{1+x^2}=-\frac{\mathrm{d}y}{1+y^2}\tag{3} $$ Furthermore, $(2)$ implies $$ \log\left(\frac{1+x}{\sqrt2}\right)=-\log\left(\frac{1+y}{\sqrt2}\right)\tag{4} $$ Substituting, using $(3)$ and $(4)$, remembering to flip the limits of integration, yields $$ \int_0^1\log\left(\frac{1+x}{\sqrt2}\right)\frac{\mathrm{d}x}{1+x^2}=-\int_0^1\log\left(\frac{1+y}{\sqrt2}\right)\frac{\mathrm{d}y}{1+y^2}\tag{5} $$ Noting that the left and right sides of $(5)$ are equal yet opposite, we see that both are $0$. Unraveling yields $$ \begin{align} \int_0^1\frac{\log(1+x)}{1+x^2}\mathrm{d}x &=\int_0^1\frac{\log(\sqrt2)}{1+x^2}\mathrm{d}x\tag{6} \end{align} $$ To evaluate $(6)$ note that the substitution $x\mapsto\frac1x$ yields $$ \int_0^1\frac{\mathrm{d}x}{1+x^2}=\int_1^\infty\frac{\mathrm{d}x}{1+x^2}\tag{7} $$ and since $\frac1{1+x^2}$ is even we get $$ \int_0^1\frac{\mathrm{d}x}{1+x^2}=\frac14\int_{-\infty}^\infty\frac{\mathrm{d}x}{1+x^2}\tag{8} $$ Let $\gamma$ be the contour following the real line on $[-R,R]$ and circling back counterclockwise in the upper half-plane along $|z|=R$, we get $$ \int_{-\infty}^\infty\frac{\mathrm{d}x}{1+x^2}=\int_\gamma\frac{\mathrm{d}z}{1+z^2}\tag{9} $$ There is one singularity in the upper half-plane at $z=i$ with residue $\frac1{2i}$ which means the value of the integral along $\gamma$ is $2\pi i\cdot\frac1{2i}=\pi$. Using $(6)$, $(8)$, and $(9)$, this yields $$ \begin{align} \int_0^1\frac{\log(1+x)}{1+x^2}\mathrm{d}x &=\int_0^1\frac{\log(\sqrt2)}{1+x^2}\mathrm{d}x\\ &=\log(\sqrt2)\cdot\frac14\int_{-\infty}^\infty\frac1{1+x^2}\mathrm{d}x\\ &=\log(\sqrt2)\cdot\frac14\cdot\pi\\ &=\frac\pi8\log(2)\tag{10} \end{align} $$
