Why is 2 $\cdot$ $\sin(\alpha)$ $\cos(\alpha)$=$\sin(2\alpha)$?

Question

I am solving a physics problem involving a 2-dimensional throw. However, I have hit a bump trying to understand

$$2\cdot \sin(\alpha)\cdot\cos(\alpha)=\sin(2\alpha)$$

I have googled and searched on Stack Exhange but found nothing. I hope someone can explain how those two equal each other.

Also: "Using the unit circle to prove the double angle formulas for sine and cosine?" — Blue, Dec 11 '18 at 22:45
You don’t need dollar signs around each individual math symbol. — Randall, Dec 11 '18 at 22:45
@Damien I like the way you think, but if you don't know the angle addition rules, I am not sure you are ready for De Moivre's law. — Doug M, Dec 11 '18 at 23:03
Most of these trig identities can be derived rather quickly using the definition of $\sin$ and $\cos$ from a complex number perspective instead of the usual geometric perspective, something which sadly is not taught early enough in my opinion (not least of all in part due to students fear of complex numbers in the first place). You should know that $\sin(z) = \dfrac{e^{iz} - e^{-iz}}{2i}$ and that $\cos(z) = \dfrac{e^{iz}+e^{-iz}}{2}$. Taking these forms of the expressions and comparing $2\sin(\alpha)\cos(\alpha)$ to $\sin(2\alpha)$ should give the result. — JMoravitz, Dec 11 '18 at 23:04

Doug M · Accepted Answer · 2018-12-11T23:01:33.840

9

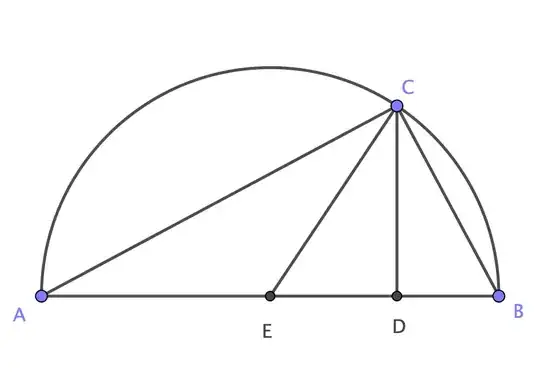
Here is one visualization.

The area of the red triangle is $\frac 12 bh$

the base is $1,$ the height is $\sin 2a$

$A = \frac 12 \sin 2a$

But is can also be decomposed into 2 congruent right triangles with legs $\cos a, \sin a$

$A = \cos a\sin a$

$\frac 12 \sin 2a = \cos a\sin a\\ \sin 2a = 2\cos a\sin a$

Here is another.

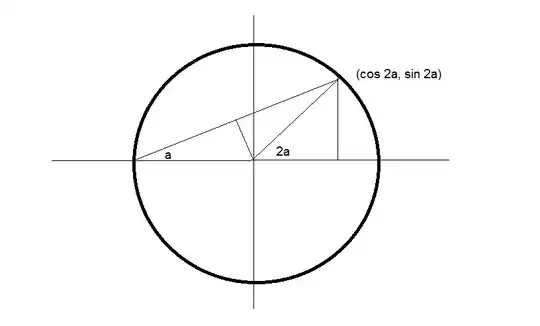
The hypotenuse of the triangle with vertexes $(-1,0), (\cos 2a, \sin 2a)$ is $2\cos a$

$\sin a = \frac {\text{opposite}}{\text{hypotenuse}} = \frac {\sin 2a}{2\cos a}\\ 2\sin a\cos a = \sin 2a$

Or you can be really boring and say that is falls out of the angle addition rules

$\sin 2a = \sin (a+a) = \sin a\cos a + \cos a\sin a$

edited Dec 11 '18 at 23:01

answered Dec 11 '18 at 22:56

Doug M

57,877

Very pretty indeed, *+1, endorsed!!!* – Robert Lewis Dec 11 '18 at 23:06
+1
Thanks I know understand where its from. However could you quickly explain how cos(a)*sin(a)= A

Thanks again
– Hamzalihi Dec 11 '18 at 23:11
We can look at the red area as 2 right triangles each with legs $\cos a, \sin a$ or as an isosceles triangle with base $2\sin a$ and altitude $\cos a$ if you prefer. If you think of it as 2 right triangles then the area is $2(\frac 12 \sin a\cos a)$ or one isosceles triangle $\frac12 (2\sin a)(\cos a)$ – Doug M Dec 11 '18 at 23:15
ok. If we multiply in then 2(1/2 sin(a) cos(a) ) it would be sin(a)cos(a) because 2*1/2 gives one ? – Hamzalihi Dec 11 '18 at 23:23
@Hamilton Yes, that's it. Just twice the area of one small triangle. – timtfj Dec 11 '18 at 23:31
Trig identities are always much friendlier in visual form! (OK, now sonene will provide a counterexample). – timtfj Dec 11 '18 at 23:34

score 3 · Answer 2 · answered Dec 11 '18 at 23:11

Consider the semicircle over the diameter $[AB]$ of radius 1 and center $E$. Let $C$ be an arbitrary point on the semicircle and $D$ the foot of the altitude of the side $[AB]$ in the triangle $\Delta ABC$. Denote furthermore by $\alpha$ the angle $\angle BAC$. It follows that $\angle BEC=2\alpha$.

By the definition of the sine and cosine $$\sin(\alpha)=\frac{[CB]}{[AB]}$$ $$\cos(\alpha)=\frac{[AC]}{[AB]}$$ Thus $$\sin(\alpha)·\cos(\alpha)=\frac{[CB]·[AC]}{[AB]^2}$$

Now, since $[CD]·[AB]=[AC]·[CB]$ (different ways to get the area of $\Delta ABC$)

$$\sin(\alpha)·\cos(\alpha)=\frac{[CB]·[AC]}{[AB]^2}=\frac{[CD]}{[AB]}=\frac{[CD]}{2}$$ $$\Rightarrow 2·\sin(\alpha)·\cos(\alpha)=[CD]$$

Finally $$\sin(\angle BEC)=\sin(2\alpha)=\frac{[CD]}{[EC]}=[CD] \Rightarrow \sin(2\alpha)=2·\sin(\alpha)·\cos(\alpha)$$

Robert Lewis · Answer 3 · 2018-12-11T22:57:50.917

2

This follows directly from the well-known angle-addition formula for $\sin$:

$\sin(\alpha + \beta) = (\sin \alpha)(\cos \beta) + (\sin \beta)(\cos \alpha); \tag 1$

by taking $\alpha = \beta$:

$\sin 2 \alpha = (\sin \alpha)(\cos \alpha) + (\sin \alpha)(\cos \alpha) = 2(\sin \alpha)(\cos \alpha); \tag 2$

see this wikipedia page.

This formula and others may also be derived from the Euler identity

$e^{i\phi} = \cos \phi + i \sin \phi \tag 3$

by taking $\phi = \alpha + \beta$; we obtain

$\cos (\alpha + \beta) + i \sin( \alpha + \beta) = e^{i(\alpha + \beta)} = e^{i\alpha}e^{i\beta} = (\cos \alpha + i \sin \alpha)(\cos \beta + i\sin \beta)$ $= (\cos \alpha)(\cos \beta) - (\sin \alpha)(\sin \beta) + i ((\sin \alpha)(\cos \beta) + (\sin \beta)(\cos \alpha)) , \tag 4$

and look at the real and imaginary parts.

and

edited Dec 11 '18 at 22:57

answered Dec 11 '18 at 22:44

Robert Lewis

71,180

1

ok. I got how you got (2) but now but I dont understand how you got (1). How does sin go into cos? – Hamzalihi Dec 11 '18 at 22:54
@Hamzalihi: check out the link to the wiki page. It explains everything. Formula (1) may be had geometrically, or by using the Euler formula as I did here. Cheers! – Robert Lewis Dec 11 '18 at 22:59

Why is 2 $\cdot$ $\sin(\alpha)$ $\cos(\alpha)$=$\sin(2\alpha)$?

3 Answers3