Boy-Girl probability question

Question

You call to someone's house and asked if they have two children. The answer happens to be yes. Then you ask if one of their children's name a William. The answer happens to be yes again.(We assume William is a boy's name, and that it's possible that both children are Williams) What's the probability that the second child is a boy?

Answer 1

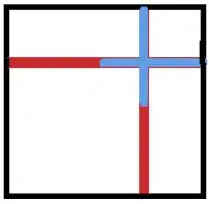
The probability is $\dfrac{1-p}{2-p}$, where $p<0.5$ is the probability that a child’s name is William. Represent the sample space of one child’s gender and name by $I$, a unit interval where numbers from $0$ to $0.5$ represent girls and numbers from $0.5$ to $1$ represent boys. Assume that like names are contiguous within the gender range, so there is a subinterval of width $p$ within $[0.5,1]$ that represents Williams.

The two children correspond to some point $(x,y)$ in $I\times I$. Knowing nothing other than that the family has (exactly) two children puts no restriction on $(x,y)$. However, if you know one child is a William, you must be in the colored cross-shaped region shown in the picture. Within that region, the red area represents one-boy-and-one-girl families, and the blue area represents two-boy families.

The probability that you are in the blue region, given that you are in the cross-shaped region, is the quotient of areas blue/cross, or $\dfrac{p-p^2}{2p-p^2}$.

Answer 2

For sake of argument suppose $1$ in $m$ boys (but no girls) are named william. And for sake of argument in every family has two children and one of the children is soaked in skunk urine to tell it apart for the other.

$\frac 12*\frac 12$ of all families have two girls. None of them named william.

$\frac 12*\frac 12=\frac 14$ of all families has one girl soaked in skunk urine and a clean boy.

So these families $\frac 1m$ of them have the boy named william.

So $\frac 1{4m}$ have a skunk urine girl and a boy named william and the other a girl.

$\frac 12*\frac 12=\frac 14$ of all families has one girl clean and one boy soaked in skunk urine. Of these $\frac 1{m}$ have a boy named william.

So $\frac 1{4m}$ has skunk urine boy named william and the other a girl.

$\frac 12*\frac 12 = \frac 14$ of all families have two boys.

$\frac 1{m^2}$ or $\frac 1{4m^2}$ of all families, of these both are named william.

$\frac 1{m}\frac {m-1}m$ or $\frac {m-1}{4m^2}$ of all, of these the skunk urine one is called william and the other isn't.

$\frac {m-1}m\frac 1{m}$ or $\frac {m-1}{4m^2}$ of all, of the the clean boy is called william that the other isn't.

So $\frac 1{4m^2} + \frac {m-1}{4m^2} + \frac {m-1}{4m^2}= \frac {2m-1}{4m^2}$ of all families has a child name william and the other a boy.

And $\frac 1{4m}+\frac 1{4m}=\frac 1{2m} = \frac {2m}{4m^2}$ of all families have a child named william and the other a girl.

And there are $\frac 1{4m^2} + \frac {m-1}{4m^2} + \frac {m-1}{4m^2}+\frac 1{4m}+\frac 1{4m} = \frac {4m -1}{4m^2}$ of all families has a child named william.

So the probability of a family with two children, one william, having two boys is

$\frac {\frac {2m-1}{4m^2}}{\frac {4m-1}{4m^2}} = \frac {2m-1}{4m-1}\approx \frac 12$ (depending on how rare william is as a name)

and the probability of having a boy and a girl is $\frac {2m}{4m-1}\approx \frac 12$.

....

There is a well known paradox that if a family with two children have at least one boy what is the probability that "the other" is a boy, or in other words what is the probability that they have two boys.

The answer is $\frac 13$. This is because of the four possible outcomes, BB, BG, GB, GG, the GG is thrown away. SO of the three equally likely outcomes only one is $BB$.

But this question is worded differently. we are told specifically that a certain one of them is a boy, not just any of them.

(Let's assume they aren't both named william).

So of the four possibilities: William is a Boy: Boy, William is Boy: Girl, William is a girl:Boy, William is girl; Girl. Now 2 of them are thrown away and only William is a Boy: Boy, William is Boy: Girl are left. So the probability is now $\frac 12$.

Answer 3

These questions are actually a lot of fun. Thank you for posting this!

A related question to this question is this:

You call households that have exactly two children. You ask whether one child is a boy. What is the probability that the second child is a boy.

Let A be the event that both children are girls, B the event that the first-born is a boy, the second-born a girl, C the event that the first-born is a girl the second-born a boy. and D the event that both children are boys. Then Events A,B,C,D are mutually disjoint and each occur with probability $\frac{1}{4}$.

Let us assume that, instead of asking if one child is a boy, you ask if the first-born is a boy. They will say yes if either Events B or D occured. Then the probability that the second-born is a boy, given that the first-born is a boy (i.e., it was Event D that occurred given that one of D or B occurred), is 1/2.

But you are actually calling and asking if one child is a boy, and they will say yes if Events B,C, or D occurred. The only households that will say no are those for which event A occurred. So the probability that the other child is a girl, given that one child is a boy, is the probability of either Event B or Event C happening given that one of Events B,C,D happened. So the probability that the other child is a girl is 2/3.

---

However, the above question is not equivalent to the original question. That only a small fraction William (as in about every other name). Here households with two boys will say yes at almost twice the rate that households will say yes to the question of "do you have a William", instead of at the same rate before. So as the fraction $p$ of Williams goes to 0, the probability that the 2nd child is a boy goes to 1/2. The calculations were already done in the other answers.

Answer 4

The crux of this problem is that the probability changes whether we find out that one of the children is William before or after we draw the family. See this paper for details. Assume that both sexes are equiprobable and that the probability of a child being a William is $p$. Denote Williams by $BW$ and male non-Williams by $B'$.

$$\begin{array}{|c|c|c|} \hline \text{Child 1} & \text{Child 2}&\text{P(Both Children)}\\ \hline BW&BW &p^2\\ \hline BW&B'&p\left(\frac12-p\right)\\ \hline BW&G&\frac12p\\ \hline B'&BW&p\left(\frac12-p\right)\\ \hline B'&B'&\left(\frac12-p\right)^2\\ \hline B'&G&\frac12\left(\frac12-p\right)\\ \hline G&BW&\frac12p\\ \hline G&B'&\frac12\left(\frac12-p\right)\\ \hline G&G&\frac14\\ \hline \end{array}\\ $$

In this space, we can see that the probability of child $2$ being a boy after we've found out that child $1$ is a William is $P(B|W)=\frac{P(B\land W)}{P(W)}=\frac1p\frac{p^2+p\left(\frac12-p\right)}{p^2+2p(1/2-p)+p+(1/2-p)^2+(1/2-p)+(1/2)^2}=\frac12$.

However, if we knew that the family had a William but not specifically that child $1$ was a William, we would have the following space.

\begin{array}{|c|c|} \hline \text{Child 1} & \text{Child 2} &\text{P(Both Children)}\\ \hline BW&BW&p^2\\ \hline BW&B'&\left(\frac12-p\right)p\\ \hline BW&G&\frac12p\\ \hline B'&BW&\left(\frac12-p\right)p\\ \hline G&BW&\frac12p\\ \hline \end{array}

So then the probability of the other child being a boy becomes $\frac{p^2+\left(\frac12-p\right)p+\left(\frac12-p\right)p}{p^2+\left(\frac12-p\right)p+\frac12p+\left(\frac12-p\right)p+\frac12p}=\frac{1-p}{2-p}$, which agrees with @Steve_Kass's answer. This is a variant of the well known paradox whose solution depends on the exact phrasing of the problem. In essence, the prior knowledge of changes the system.