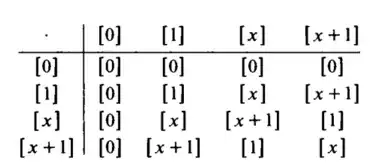$F_2$ is polynomial field of group of integer modulo $2.f(x)$ is $x^2 + x + 1$.
I didn't got how the multiplication is happening in the table.I referred to many sources related to this topic but still i am facing difficulty in understanding it.I will be very thankful if someone explains the concept behind it.
This is the multiplication table for the field ${\Bbb F}_4 = {\Bbb F}_2[x]/\langle x^2+x+1\rangle$ consisting of the residue classes of the elements $0,1,x,x+1$ which are the remainders of ${\Bbb F}_2[x]$ modulo $x^2+x+1$.
For instance, $[x] \cdot [x+1] = [x\cdot(x+1)] = [x^2+x]$ and the residue class of $x^2+x$ modulo $x^2+x+1$ is $[1]$, i.e., $x^2+x = 1\cdot (x^2+x+1) + 1$ with quotient $q(x)=1$ and remainder $r(x)=1$. This is an elementary way to view this field extension.
Here are all 4x4 operations done to fill in the multiplication table. I will write $X$ for the transcendent variable of the polynomial ring $\Bbb F_2[X]$ over the field $\Bbb F_2$ with two elements, and $x$ for the class $[X]$ which is $X$ modulo $X^2+X+1$ (irreducible=prime in the polynomial ring).
( 0 )*( 0 ) = [ 0 ] * [ 0 ] = [ 0 ] = 0
( 0 )*( 1 ) = [ 0 ] * [ 1 ] = [ 0 ] = 0
( 0 )*( x ) = [ 0 ] * [ X ] = [ 0 ] = 0
( 0 )*(x + 1) = [ 0 ] * [X + 1] = [ 0 ] = 0
( 1 )*( 0 ) = [ 1 ] * [ 0 ] = [ 0 ] = 0
( 1 )*( 1 ) = [ 1 ] * [ 1 ] = [ 1 ] = 1
( 1 )*( x ) = [ 1 ] * [ X ] = [ X ] = x
( 1 )*(x + 1) = [ 1 ] * [X + 1] = [ X + 1 ] = x + 1
( x )*( 0 ) = [ X ] * [ 0 ] = [ 0 ] = 0
( x )*( 1 ) = [ X ] * [ 1 ] = [ X ] = x
( x )*( x ) = [ X ] * [ X ] = [ X^2 ] = x + 1
( x )*(x + 1) = [ X ] * [X + 1] = [X^2 + X] = 1
(x + 1)*( 0 ) = [X + 1] * [ 0 ] = [ 0 ] = 0
(x + 1)*( 1 ) = [X + 1] * [ 1 ] = [ X + 1 ] = x + 1
(x + 1)*( x ) = [X + 1] * [ X ] = [X^2 + X] = 1
(x + 1)*(x + 1) = [X + 1] * [X + 1] = [X^2 + 1] = x
In the few ($2\times 2=4$) cases where $[X^2+\dots]$ appears as a result of computing the product of two polynomials of degree one (representing thus $x,x+1$ in $\Bbb F_2[X]$) we replace above $X^2$ by $X^2-(X^2+X+1)=-X-1=X+1$ (working modulo $X^2+X+1$.)
P.S. The above was produced by computer, it is good to know that such computation can be done, assisted and learned in this way. Used sage code:
sage: F = GF(2)
sage: R.<X> = PolynomialRing(F)
sage: K.<x> = R.quotient( X^2 + X + 1 )
sage: elements = [ K(0), K(1), x, x+1 ]
sage: for a in elements:
....: for b in elements:
....: A, B = a.lift(), b.lift()
....: print( "({:^5})*({:^5}) = [{:^5}] * [{:^5}] = [{:^7}] = {}"
....: .format(a, b, A, B, A*B, a*b) )
....: print
....:
