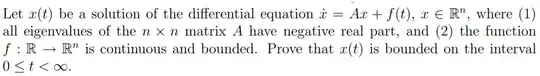In this problem, I tried the following: First I show that $$x(t) = e^{tA}x_0 + \int\limits_0^t e^{(t-s)A}f(s)ds$$ Then I take the norm for both sides $$\|x(t)\|\leq Ke^{-\alpha t}\|x_0\|+\left\|\int\limits_0^t e^{(t-s)A}f(s)ds\right\|$$ I have used Meiss’s Lemma ($\|e^{tA}\|\leq K e^{-\alpha t}\|$ for some $K>0$, $\alpha >0$).
Could you please help me in what is remaining, and if there is any mistake. Thanks.