TL;DR: For a large series of precise 3D coordinates that describe a real-world orbit, how can we determine if they all lie exactly on a plane?
The Problem
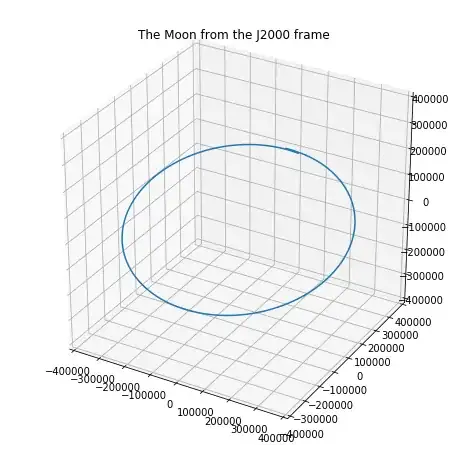
I've used NASA's highly precise SPICE toolkit to calculate the hourly position of the moon relative to the Earth in Cartesian coordinates. The frame of reference for these points is the J2000 frame: Earth's equator (x and y), with the z-axis running orthogonally through the poles.
We know the moon's orbit does not lie on the equatorial plane. The Earth-Moon orbit is typically described as a plane that is 5.14 degrees inclined from the equatorial plane.
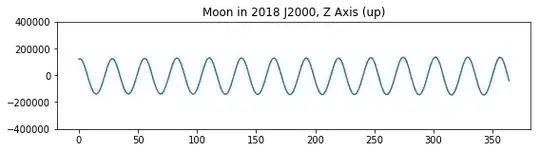
(This is a 28-day period from Jan. 2018, hence the small overlap since the sidereal month is 27.32 days.)
What I want to determine is whether this orbit is perfectly "flat" -- whether the Moon orbits the Earth on a perfect plane rotated from the terrestrial equator -- or whether there is even a slight variance on the z axis of this approximate Earth-Moon orbital plane.
It's certainly very close to a plane, as we'd expect, as you can see from a year's worth of z coordinates from the Earth's frame of reference. But orbit's are hugely complicated given all the possible aberrations, which the SPICE toolkit usually accounts for.
One idea I had was to choose three points in the orbit, spaced about 9 days apart, calculate the plane for those three points, and then calculate the distance from that plane for each point. This seems inelegant and possibly biased by which three points I choose, though in theory all I need to know is whether the distance of each point to the 3-point plane is zero, regardless of which three points define the plane.
It seems to me there is a more elegant solution than this brute-force approach?