1

The commutative law of multiplication states that:

If '$a$' and '$b$' are any whole numbers, then '$a · b = b · a$'.

I've been looking for why multiplication has this property and how is saying that 3 times 4 the same thing as saying 4 times 3. I've found two interpretations:

  1. $3 \cdot 4 = 12$ and $4 \cdot 3 = 12$ so, $3 \cdot 4 = 4 \cdot 3$,
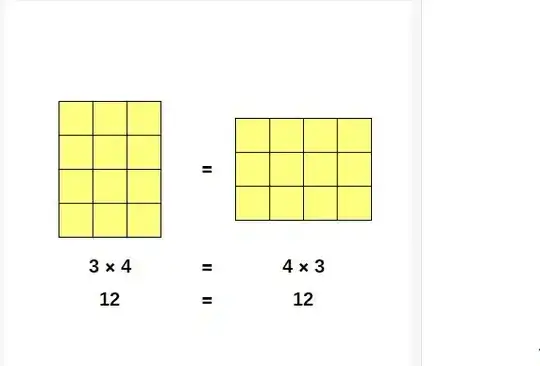
  2. Think of $3\times 4$ as the area of a rectangle with width $4$ and height $3$. If you rotate the rectangle by $90^\circ$, the area is unchanged, but now the width is $3$, and the height is $4$. So, $3\times4 =$ area of rectangle = area of rotated rectangle $= 4\times3$.enter image description here

These explanations don't seem to show why multiplication has this property but are showing us a way to make it intuitive and, thus, accept it as common sense.

Is there a better way to show that multiplication is fundamentally commutative?

Tianlalu
  • 5,177
Ashraf Benmebarek
  • 191
  • 6
  • Consider eggs or pebbles in rows : four rows of three eggs vs three rows of four eggs. – Mauro ALLEGRANZA Dec 01 '18 at 16:25
  • That's just the angle you're looking at it. In any case, multiplication is a heck of a lot more commutative than subtraction or division, e.g., $$\frac{3}{4} < \frac{4}{3}.$$ – Robert Soupe Dec 02 '18 at 06:01

2 Answers2

1

a * b = $\sum_{n=1}^b a$ = (a / b) (b / a) $\sum_{n=1}^b a$ = (a / b) $\sum_{n=1}^b b$ = $\sum_{n=1}^a b$ = b * a

For example, 3 * 4 = 3 + 3 + 3 + 3 = (3 / 4) (4 / 3) (3 + 3 + 3 + 3) = (3 / 4) (4 + 4 + 4 + 4) = 4 + 4 + 4 = 4 * 3

In words, 3 * 4 is 3 added 4 times (3 + 3 + 3 + 3). If you take 4/3 of that, all the 4s become 3s (4 + 4 + 4 + 4). In order to keep the expression constant, you need to multiply by 3/4. Since there are 4 4s in (4 + 4 + 4 + 4), 3/4 of that is just 3 4s (4 + 4 + 4), which is 4 added 3 times or 4 * 3.

Taylor
  • 11
0

We can actually consider the geometric interpretation to be rigorous if we define operations on whole numbers purely from a geometric stand-point, where we would have an axiom stating that the rotation of an object does not change its area.

For a proof based on the Peano Axioms, look at the following link On the commutative property of multiplication (domain of integers, possibly reals).

modest_mildew
  • 9