It is well known that the fourier series for $e^{\cos(\theta)}\sin(\sin(\theta))$ is $\sum_{n=1}^\infty \frac{\sin(n\theta)}{n!}$ which implies that
$$\int_{-\pi}^\pi e^{\cos(\theta)}\sin(\sin(\theta))\sin(n\theta)dx=\frac{\pi}{n!}$$ for $n>0$. My question is if this identity can be extended to fractional values such as $$\int_{-\pi}^\pi e^{\cos(\theta)}\sin(\sin(\theta))\sin(\frac{\theta}{2})d\theta=2\sqrt{\pi} $$
Incomplete answer: only numerical experiments.
Let me define $$ s(n) = \int_{-\pi}^\pi e^{\cos\theta}\sin(\sin\theta)\sin(n\theta)\,d\theta $$ and $$ g(n) = \frac{s(n)-\frac{\pi}{\Gamma(n+1)}}{\sin\bigl((n-1)\pi\bigr)}. $$ Numerical evidence suggests that $g(n)\to0$; but how fast? Let's try to extract some more information.
Here I plot $-\log\bigl(g(n)\bigr)$ for $n\in[1,20]$:
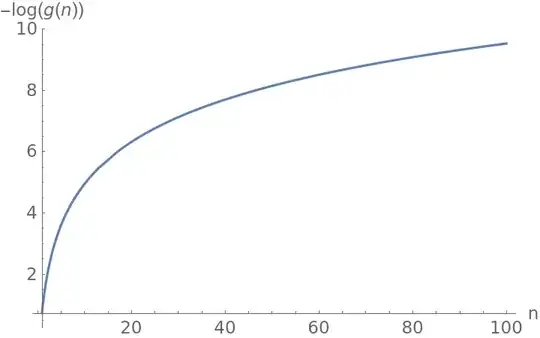
It looks like a logarithm, so it seems natural to try to fit it with $$ -\log\bigl(g(n)\bigr) = a+b\log(n+c). $$
By fiddling a bit (and looking at larger ranges of $n$) one can see that $b$ has to be $2$, so we have $a+2\log(n+c)$. The value $g(1)$ seems to be around $0.5$, a bit less, so we impose $a+2\log(1+b)=\log(2)$. Moreover, by looking at large values, we deduce that $a=1-\log(2)$ seems a good value. Therefore our approximation is $$ g(n) \simeq \frac{2}{\bigl(2+\sqrt e(n-1)\bigr)^2}, $$ which leads to $$ s(n) \simeq \frac{\pi}{\Gamma(n+1)} + \frac{2\sin\bigl((n-1)\pi\bigr)}{\bigl(2+\sqrt e(n-1)\bigr)^2} . $$
